Create a new header file named likelihood.hpp containing the following code.
#pragma once
#include <map>
#include <boost/algorithm/string.hpp>
#include <boost/format.hpp>
#include <boost/shared_ptr.hpp>
#include <boost/range/adaptor/reversed.hpp>
#include "libhmsbeagle/beagle.h"
#include "tree.hpp"
#include "data.hpp"
#include "xstrom.hpp"
namespace strom {
class Likelihood {
public:
Likelihood();
~Likelihood();
void setRooted(bool is_rooted);
void setPreferGPU(bool prefer_gpu);
void setAmbiguityEqualsMissing(bool ambig_equals_missing);
bool usingStoredData() const;
void useStoredData(bool using_data);
std::string beagleLibVersion() const;
std::string availableResources() const;
std::string usedResources() const;
void initBeagleLib();
void finalizeBeagleLib(bool use_exceptions);
double calcLogLikelihood(Tree::SharedPtr t);
Data::SharedPtr getData();
void setData(Data::SharedPtr d);
void clear();
unsigned calcNumEdgesInFullyResolvedTree() const;
unsigned calcNumInternalsInFullyResolvedTree() const;
private:
struct InstanceInfo {
int handle;
int resourcenumber;
std::string resourcename;
unsigned nstates;
unsigned nratecateg;
unsigned npatterns;
unsigned partial_offset;
unsigned tmatrix_offset;
std::vector<unsigned> subsets;
InstanceInfo() : handle(-1), resourcenumber(-1), resourcename(""), nstates(0), nratecateg(0), npatterns(0), partial_offset(0), tmatrix_offset(0) {}
};
typedef std::pair<unsigned, int> instance_pair_t;
unsigned getScalerIndex(Node * nd, InstanceInfo & info) const;
unsigned getPartialIndex(Node * nd, InstanceInfo & info) const;
unsigned getTMatrixIndex(Node * nd, InstanceInfo & info, unsigned subset_index) const;
void updateInstanceMap(instance_pair_t & p, unsigned subset);
void newInstance(unsigned nstates, int nrates, std::vector<unsigned> & subset_indices);
void setTipStates();
void setTipPartials();
void setPatternPartitionAssignments();
void setPatternWeights();
void setAmongSiteRateHeterogenetity();
void setModelRateMatrix();
void addOperation(InstanceInfo & info, Node * nd, Node * lchild, Node * rchild, unsigned subset_index);
void queuePartialsRecalculation(Node * nd, Node * lchild, Node * rchild);
void queueTMatrixRecalculation(Node * nd);
void defineOperations(Tree::SharedPtr t);
void updateTransitionMatrices();
void calculatePartials();
double calcInstanceLogLikelihood(InstanceInfo & inst, Tree::SharedPtr t);
std::vector<InstanceInfo> _instances;
std::map<int, std::string> _beagle_error;
std::map<int, std::vector<int> > _operations;
std::map<int, std::vector<int> > _pmatrix_index;
std::map<int, std::vector<double> > _edge_lengths;
std::map<int, std::vector<int> > _eigen_indices;
std::map<int, std::vector<int> > _category_rate_indices;
double _relrate_normalizing_constant;
std::vector<int> _subset_indices;
std::vector<int> _parent_indices;
std::vector<int> _child_indices;
std::vector<int> _tmatrix_indices;
std::vector<int> _weights_indices;
std::vector<int> _freqs_indices;
std::vector<int> _scaling_indices;
Data::SharedPtr _data;
unsigned _ntaxa;
bool _rooted;
bool _prefer_gpu;
bool _ambiguity_equals_missing;
bool _using_data;
public:
typedef std::shared_ptr< Likelihood > SharedPtr;
};
// member function bodies go here
}
Constructor
As in previous classes, the constructor reports (if the line was uncommented) that a Likelihood object was constructed and then calls the clear function to do the initialization work.
inline Likelihood::Likelihood() {
//std::cout << "Constructing a Likelihood" << std::endl;
clear();
}
Destructor
inline Likelihood::~Likelihood() {
//std::cout << "Destroying a Likelihood" << std::endl;
finalizeBeagleLib(false);
clear();
}
The destructor calls the function finalizeBeagleLib to tell BeagleLib that our program is shutting down and its services will no longer be needed. If for some reason BeagleLib cannot shut down cleanly, an error message is output so that the user is informed. While it may be tempting to throw an XStrom exception here, C++11 implicitly assumes that destructors do not throw exceptions. Thus we avoid throwing an exception here (by passing false to the finalizeBeagleLib function) while still warning the user that something unusual happened.
The calcNumEdgesInFullyResolvedTree member function
This function returns the number of edges in a binary tree, taking into account whether the tree is rooted. This is used to allocate the correct amount of memory in BeagleLib for storing transition probability matrices.
inline unsigned Likelihood::calcNumEdgesInFullyResolvedTree() const {
assert(_ntaxa > 0);
return (_rooted ? (2*_ntaxa - 2) : (2*_ntaxa - 3));
}
The calcNumInternalsInFullyResolvedTree member function
This function returns the number of internal nodes in a binary tree, taking into account whether the tree is rooted. This is used to allocate the correct amount of memory in BeagleLib for partial likelihood arrays.
inline unsigned Likelihood::calcNumInternalsInFullyResolvedTree() const {
assert(_ntaxa > 0);
return (_rooted ? (_ntaxa - 1) : (_ntaxa - 2));
}
The finalizeBeagleLib member function
This is used to shut down all active BeagleLib instances and erase the _instances vector. This function is called by the Likelihood constructor (via the clear member function) and destructor, and is also called by the initBeagleLib function to ensure that no instances already exist before creating new ones. The parameter use_exceptions is necessary because exceptions should not be thrown by a destructor (an implicit assumption in C++11); in this case, any error messages produced by BeagleLib need to be output using the standard error stream rather than by throwing an exception.
inline void Likelihood::finalizeBeagleLib(bool use_exceptions) {
// Close down all BeagleLib instances if active
for (auto info : _instances) {
if (info.handle >= 0) {
int code = beagleFinalizeInstance(info.handle);
if (code != 0) {
if (use_exceptions)
throw XStrom(boost::format("Likelihood failed to finalize BeagleLib instance. BeagleLib error code was %d (%s).") % code % _beagle_error[code]);
else
std::cerr << boost::format("Likelihood destructor failed to finalize BeagleLib instance. BeagleLib error code was %d (%s).") % code % _beagle_error[code] << std::endl;
}
}
}
_instances.clear();
}
The clear member function
The clear function of the Likelihood class is a little more complex than for previous classes because it creates the _beagle_error map.
inline void Likelihood::clear() {
finalizeBeagleLib(true);
_ntaxa = 0;
_rooted = false;
_prefer_gpu = false;
_ambiguity_equals_missing = true;
_using_data = true;
_data = nullptr;
_operations.clear();
_pmatrix_index.clear();
_edge_lengths.clear();
_eigen_indices.clear();
_category_rate_indices.clear();
_relrate_normalizing_constant = 1.0;
_subset_indices.assign(1, 0);
_parent_indices.assign(1, 0);
_child_indices.assign(1, 0);
_tmatrix_indices.assign(1, 0);
_weights_indices.assign(1, 0);
_freqs_indices.assign(1, 0);
_scaling_indices.assign(1, 0);
// Store BeagleLib error codes so that useful
// error messages may be provided to the user
_beagle_error.clear();
_beagle_error[0] = std::string("success");
_beagle_error[-1] = std::string("unspecified error");
_beagle_error[-2] = std::string("not enough memory could be allocated");
_beagle_error[-3] = std::string("unspecified exception");
_beagle_error[-4] = std::string("the instance index is out of range, or the instance has not been created");
_beagle_error[-5] = std::string("one of the indices specified exceeded the range of the array");
_beagle_error[-6] = std::string("no resource matches requirements");
_beagle_error[-7] = std::string("no implementation matches requirements");
_beagle_error[-8] = std::string("floating-point range exceeded");
}
The function first ensures that no instances of BeagleLib exist by calling finalizeBeagleLib.
The _beagle_error map simply stores BeagleLib error codes (cryptic negative integers) and associates them with meaningful messages so that your users have some chance of knowing what went wrong if BeagleLib fails. The constructor fills the map with all possible error codes so that we are ready for any error code that BeagleLib can spit out.
The beagleLibVersion, availableResources, and usedResources member functions
The beagleLibVersion function is useful for obtaining the version of BeagleLib being used. The availableResources function queries BeagleLib and returns a string listing resources, which will include only the CPU resource unless you are using a machine that is set up for GPU processing.
inline std::string Likelihood::beagleLibVersion() const {
return std::string(beagleGetVersion());
}
inline std::string Likelihood::availableResources() const {
BeagleResourceList * rsrcList = beagleGetResourceList();
std::string s;
for (int i = 0; i < rsrcList->length; ++i) {
std::string desc = rsrcList->list[i].description;
boost::trim(desc);
if (desc.size() > 0)
s += boost::str(boost::format(" resource %d: %s (%s)\n") % i % rsrcList->list[i].name % desc);
else
s += boost::str(boost::format(" resource %d: %s\n") % i % rsrcList->list[i].name);
}
boost::trim_right(s);
return s;
}
inline std::string Likelihood::usedResources() const {
std::string s;
for (unsigned i = 0; i < _instances.size(); i++) {
s += boost::str(boost::format(" instance %d: %s (resource %d)\n") % _instances[i].handle % _instances[i].resourcename % _instances[i].resourcenumber);
}
return s;
}
The getData and setData member functions
These functions allow you to associate a Data object with this Likelihood object. Note that the data to be used should be established before initBeagleLib is called, as the instances of BeagleLib created depend on the number of states and patterns in the data, hence the assert that checks to see that no BeagleLib instances exist.
inline Data::SharedPtr Likelihood::getData() {
return _data;
}
inline void Likelihood::setData(Data::SharedPtr data) {
assert(_instances.size() == 0);
assert(!data->getDataMatrix().empty());
_data = data;
}
The setRooted member function
Sets the _rooted data member, which determines whether trees are to be considered rooted (true) or unrooted (false). The rooting status cannot be changed after BeagleLib instances are created in initBeagelLib, hence the assert that checks to see that no BeagleLib instances exist. If this function is called when _rooted is already equal to is_rooted, then the function call is a no-op (“no operation”), meaning that it has no effect. In this case, it does not matter whether BeagleLib instances have been created; the second part of the assert prevents the assert from tripping in such cases.
inline void Likelihood::setRooted(bool is_rooted) {
assert(_instances.size() == 0 || _rooted == is_rooted); // can't change rooting status after initBeagleLib called
_rooted = is_rooted;
}
The setPreferGPU member function
Sets the _prefer_gpu data member, which determines whether BeagleLib should use GPU resources (true) or just the CPU version of the library (false). The GPU status cannot be changed after BeagleLib instances are created in initBeagelLib, hence the assert that checks to see that either no BeagleLib instances exist or that the call is a no-op.
inline void Likelihood::setPreferGPU(bool prefer_gpu) {
// Can't change GPU preference status after initBeagleLib called
assert(_instances.size() == 0 || _prefer_gpu == prefer_gpu);
_prefer_gpu = prefer_gpu;
}
The setAmbiguityEqualsMissing member function
Sets the _ambiguity_equals_missing data member, which determines whether ambiguous states in the data are treated as if they were completely missing data. Treating ambiguities as missing data is both considerably faster computationally and requires less memory because states for tips can be stored directly rather than in the form of partial likelihood arrays.
inline void Likelihood::setAmbiguityEqualsMissing(bool ambig_equals_missing) {
// Can't change GPU preference status after initBeagleLib called
assert(_instances.size() == 0 || _ambiguity_equals_missing == ambig_equals_missing);
_ambiguity_equals_missing = ambig_equals_missing;
}
The useStoredData member function
This function allows you to toggle whether data stored is actually used when computing the likelihood. If _using_data is false (done by calling useStoredData(false)), the calcLogLikelihood function simply returns 0.0 and does not bother to compute anything. This will be useful for forcing an MCMC analysis to explore the prior distribution rather than the posterior distribution.
inline void Likelihood::useStoredData(bool using_data) {
_using_data = using_data;
}
The usingStoredData member function
This function allows you to determine whether data stored is being used when computing the likelihood. It simply returns the current value of _using_data.
inline bool Likelihood::usingStoredData() const {
return _using_data;
}
Graphical overview for the unpartitioned case
Before diving into calling the BeagleLib functions that will set the stage for a likelihood calculation, it is useful to know the big picture. The figure below illustrates all the memory that must be allocated by BeagleLib before the likelihood can be computed. The example illustrated involves 5 taxa and only 8 sites (3 data patterns), with no data partitioning. The model is Jukes-Cantor with no rate heterogeneity. (PDF version of this figure)
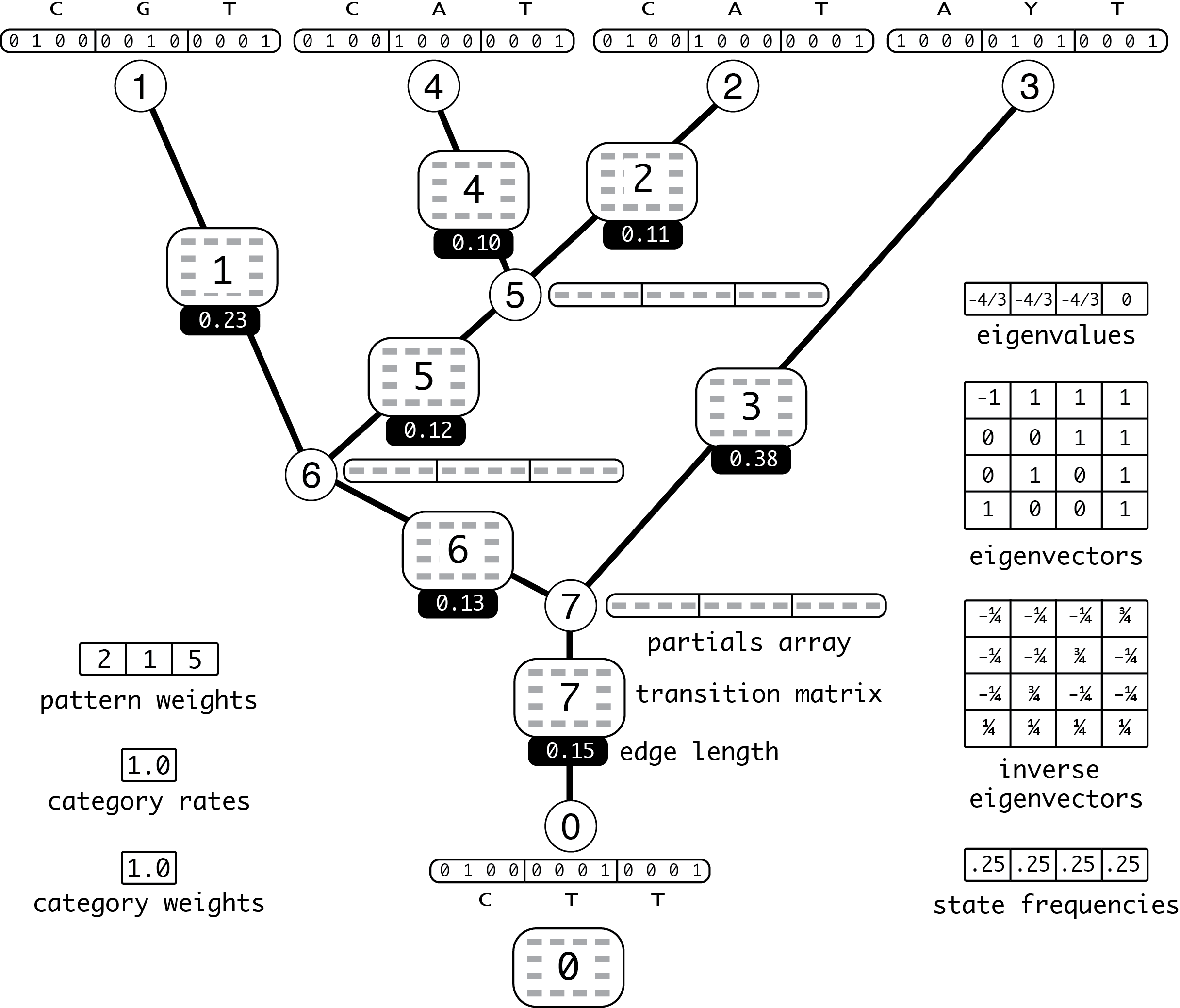
Figure 10.1: Unpartitioned example
Seven transition probability matrices are needed (one for each edge); however, 8 are allocated within BeagleLib. The transition matrix corresponding to the root node (0) will not be used, which introduces a slight inefficiency but has the benefit that the transition matrix used for a node can be easily determined from the node number (no exception needs to be made for the branch directly above the root node). These 8 transition matrices are labeled with their indices (0,1,…,7). Each of these transition matrices is determined by a common eigensystem (eigenvectors and their corresponding eigenvalues), a common set of state frequencies (all 0.25 for the JC model), and the length of the edge to which the transition probability matrix belongs. There are 8 partials arrays (one for each node) and the partials arrays corresponding to leaf nodes (including the root, which is a leaf in this unrooted tree) are filled in with values corresponding to the 3 observed data patterns.
Graphical overview for the partitioned case
Here is the same example data but with a partition defined that separates the data into two subsets, with the first 2 patterns in subset 0 and the third pattern in subset 1. Here is an example of a NEXUS-formatted data block and trees block consistent with the example. Note that the first 2 sites correspond to the first pattern, the third site corresponds to the second pattern, and the final 5 sites correspond to the third pattern. (There is of course no rule that says sites must be grouped by pattern, but I’ve contrived a data set that does that to make it easy to see the correspondence between sites and site patterns.)
#nexus
begin taxa;
dimensions ntax=5;
taxlabels taxon0 taxon1 taxon2 taxon3 taxon4;
end;
begin trees;
tree t = [&U] (taxon0:.15,taxon3:.38,(taxon1:.23,(taxon2:.11,taxon4:.10)node5:.12)node6:.13);
end;
begin data;
dimensions ntax=5 nchar=8;
format datatype=dna;
matrix
taxon0 CC T TTTTT
taxon1 CC G TTTTT
taxon2 CC A TTTTT
taxon3 AA Y TTTTT
taxon4 CC A TTTTT
;
end;
I’ve assumed a JC model for subset 0, and an F81 model with state frequencies 0.1, 0.2, 0.3, 0.4 for subset 1. Everything related to subset 1 is shown with lavender shading. This version of the example will help in understanding paths in the code that pertain to partitioned data. (PDF version of this figure)
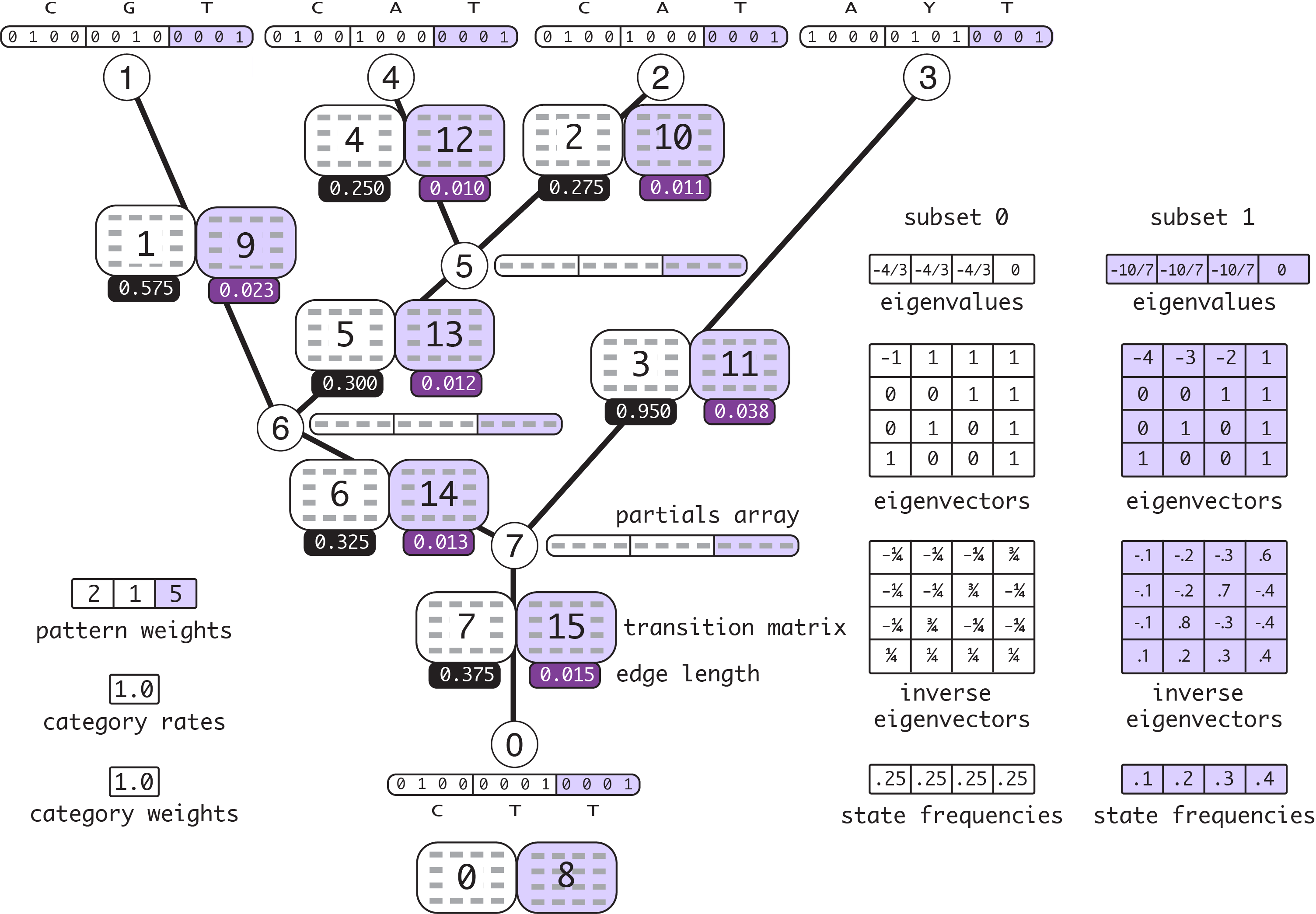
Figure 10.2: Partitioned example with 2 subsets (relative rates 2.5 and 0.1)
Note that the edge lengths have been adjusted using subset relative rates 2.5 (subset 0) and 0.1 (subset 1). These are valid (albeit arbitrary) subset relative rates because they result in a mean rate of 1.0:
2.5*(3/8) + 0.1*(5/8) = 1.0
The 3/8 and 5/8 terms in the calculation come from the fact that 3/8 of sites fall into subset 0 and 5/8 of sites fall into subset 1.
Note also that twice as many transition probability matrices are needed in this partitioned example because there are two subsets and the edge lengths (as well as the eigenvectors, eigenvalues, and state frequencies) differ for each subset. The indices for the subset 1 transition probability matrices are offset by 7 from their subset 0 counterparts because there are 8 transition matrices allocated for each subset, one for every node (see the note above about why there is not one transition matrix for every edge).
There are also two eigen decompositions and state frequency arrays needed because the substitution model differs between subsets.
Finally, we still need just one set of partials (one partial array for each node) because each partial accommodates all patterns regardless of the subset to which a pattern belongs. The part of each partial array pertaining to subset 1 is shown with lavender shading.
What does BeagleLib need?
Below is a description of all the major components that BeagleLib needs in order to compute the likelihood. Subsequent sections of this step of the tutorial each focus on the particular BeagleLib function that loads one or two of these components.
Partial likelihood arrays
Partial likelihood arrays are all of length 12 in this example (4 values are required to hold the likelihood conditional on each of the 4 nucleotide states for each of the 3 patterns). Tip partials are shown with values corresponding to the nucleotide states shown; partials at internal nodes are shown as arrays of 12 elements, but the elements are occupied by gray rectangular placeholders instead of actual values.
Edge lengths
The edge lengths are shown as white text on solid black (or purple) boxes. Note that the edge lengths for the partitioned example have already been multiplied by the appropriate subset relative rate.
Transition probability matrices
Transition probability matrices are shown as 4 by 4 matrices containing 16 gray rectangular placeholders. The index of each transition probability matrix is indicated by the number in the center.
Pattern weights
The 3 elements of this array hold the number of sites having each of the 3 patterns. In this example, the first site pattern occurs in 2 sites, the second pattern was found in only 1 site, and the third (constant) pattern was seen in 5 sites.
Category rates
The relative substitution rate equals 1.0 when there is no rate heterogeneity among sites. Relative rate 1.0 means that every site evolves at 1.0 times the average rate (where the average rate is determined by the edge lengths).
Category weights
Because we are assuming no rate heterogeneity, there is only one relative rate (1.0) and it has probability 1.0. The category weight is really the probability that a given site will experience that category’s rate. In this case, the probability is 1.0 that any given site will have relative rate 1.0.
Eigenvalues
The Jukes-Cantor (JC) and Felsenstein 1981 (F81) instantaneous rate matricies used in the examples can be decomposed by diagonalization into 4 eigenvalues, one of which equals 0 (reflecting the constraint that sequences neither grow nor shrink in length over time) with the other 3 all equal and negative, and 4 corresponding eigenvectors.
Eigenvectors
These are the right eigenvectors of the JC (and, in Fig. 10.2, also F81) instantaneous rate matrix. Even though the eigenvectors are shown here as a matrix, BeagleLib expects the eigenvector matrix to be provided as an array with 16 elements. The first 4 elements correspond to the first row of the matrix, the next 4 elements correspond to the second row of the matrix, etc.
Inverse eigenvectors
This is the inverse of the matrix of right eigenvectors. As with the eigenvector matrix, BeagleLib expects a flattened 16-element array, not a 2-dimensional array.
State frequencies
The JC model specifies equal relative state frequencies. The F81 model allows arbitrary frequencies; the values 0.1, 0.2, 0.3, and 0.4 are assumed for the F81 model in Fig. 10.2.
Tip states versus tip partials
BeagleLib handles tips in one of two ways. We are currently allocating and using tip partials to store the observed data. In the figures above, this is clear from the fact that each state at a tip (leaf node) requires 4 values, all but one of which are zero if the state is unambiguous. This requires a lot of memory (and extra computation) but allows ambiguous observed states to be handled correctly. The alternative, which is possible only if states are unambiguous or completely ambiguous (i.e. missing data), is called tip states. If using tip states, we save only a single value for each observed state (e.g. 0 for A, 1 for C, 2 for G, and 3 for T; missing data is represented by a value equal to the number of states, which is 4 for nucleotide data) and save having to sum over four values for each tip state. Using tip states can lead to quite substantial savings computationally. Remember that more than half of the nodes in a tree are tips. Later in the tutorial, we will give users of our program an option that causes all ambiguities to be treated as missing data, which makes it possible to use tip states for every tip. BeagleLib makes it possible to use tip partials for some tips (those having ambiguous states for some sites) and tip states for other tips, but we will allow only all or none for purposes of this tutorial. Setting the data member _ambiguity_equals_missing to true (its value can be set using the member function setAmbiguityEqualsMissing) forces the use of tip states by converting all partial ambiguities to be completely missing data.
Importantly, the indexing system used in BeagleLib for internal node partials is the same whether tip states or tip partials are used. You might assume that, if tip states are used, internal node partials should be indexed starting at zero rather than the number of tips, but you would be wrong! If there are 5 tips (as in the figures above), then your first internal node partial should have index 5, not 0, even if you are using tip states. Internally, BeagleLib always allocates partials vectors as if tip partials was going to be used. If tips states are used, the first (number of tips) elements of these vectors are NULL (not allocated), so using an index of 0 when tip states are being used will lead to a memory fault as there is no memory allocated for partials at index 0.
The initBeagleLib member function
The initBeagleLib member function initializes BeagleLib, obtaining one or more BeagleLib instance handles (integer values) that are stored in the vector data member _instance. Before calling this function, you will need to know details about the data subsets you plan to analyze: the number of taxa, number of states (e.g. 4 for DNA), number of unique site patterns, number of rate categories for modeling among-site rate heterogeneity, whether the tree is rooted, and whether you prefer to use GPUs or the default CPU resource if there is a choice.
Each BeagleLib instance is based on a particular fixed combination of number of states and number of rate categories. If all of your data is nucleotide and uses the same number of rate categories, then you will need only one BeagleLib instance, but if different combinations of number of states and number of rate categories exist across data subsets, then you will need to allocate multiple BeagleLib instances.
Here is the body of the initBeagleLib function. The work of actually creating instances is farmed out to the member function newInstance, so much of what you see here is devoted to simply determining how many instances are needed. A std::set named nstates_ncateg_combinations is used to determine how many unique combinations of states and rates there are. For every unique combination there is an entry in the std::map named subsets_for_pair that stores the indices of all data subsets that have that particular combination. After newInstance is called to create each instance, the function concludes by setting the information that is data-specific (doesn’t depend on any particular tree toplogy).
inline void Likelihood::initBeagleLib() {
assert(_data);
// Close down any existing BeagleLib instances
finalizeBeagleLib(true);
_ntaxa = _data->getNumTaxa();
unsigned nsubsets = _data->getNumSubsets();
std::set<instance_pair_t> nstates_ncateg_combinations;
std::map<instance_pair_t, std::vector<unsigned> > subsets_for_pair;
for (unsigned subset = 0; subset < nsubsets; subset++) {
// Create a pair comprising number of states and number of rate categories
unsigned nstates = _data->getNumStatesForSubset(subset);
int nrates = 1; // assuming no rate heterogeneity for now
instance_pair_t p = std::make_pair(nstates, nrates);
// Add combo to set
nstates_ncateg_combinations.insert(p);
subsets_for_pair[p].push_back(subset);
}
// Create one instance for each distinct nstates-nrates combination
_instances.clear();
for (auto p : nstates_ncateg_combinations) {
newInstance(p.first, p.second, subsets_for_pair[p]);
InstanceInfo & info = *_instances.rbegin();
std::cout << boost::str(boost::format("Created BeagleLib instance %d (%d states, %d rate%s, %d subset%s)") % info.handle % info.nstates % info.nratecateg % (info.nratecateg == 1 ? "" : "s") % info.subsets.size() % (info.subsets.size() == 1 ? "" : "s")) << std::endl;
}
if (_ambiguity_equals_missing)
setTipStates();
else
setTipPartials();
setPatternWeights();
setPatternPartitionAssignments();
}
The newInstance member function
This function is called by initBeagleLib to do the work of setting up individual instances. It is supplied with the number of states nstates, number of rate categories nrates, and a vector of indices of subsets that have this particular combination of nstates and nrates.
The part of the code for this function that involves the beagleCreateInstance call will be described below the code block. At the end of the function, an InstanceInfo object is created with details of this particular instance and added to the _instances vector.
inline void Likelihood::newInstance(unsigned nstates, int nrates, std::vector<unsigned> & subset_indices) {
unsigned num_subsets = (unsigned)subset_indices.size();
unsigned ngammacat = (unsigned)nrates;
unsigned num_patterns = 0;
for (auto s : subset_indices) {
num_patterns += _data->getNumPatternsInSubset(s);
}
unsigned num_internals = calcNumInternalsInFullyResolvedTree();
unsigned num_edges = calcNumEdgesInFullyResolvedTree();
unsigned num_nodes = num_edges + 1;
unsigned num_transition_probs = num_nodes*num_subsets;
long requirementFlags = 0;
long preferenceFlags = BEAGLE_FLAG_PRECISION_SINGLE | BEAGLE_FLAG_THREADING_CPP;
if (_prefer_gpu)
preferenceFlags |= BEAGLE_FLAG_PROCESSOR_GPU;
else
preferenceFlags |= BEAGLE_FLAG_PROCESSOR_CPU;
BeagleInstanceDetails instance_details;
unsigned npartials = num_internals + _ntaxa;
unsigned nsequences = 0;
if (_ambiguity_equals_missing) {
npartials -= _ntaxa;
nsequences += _ntaxa;
}
int inst = beagleCreateInstance(
_ntaxa, // tips
npartials, // partials
nsequences, // sequences
nstates, // states
num_patterns, // patterns (total across all subsets that use this instance)
num_subsets, // models (one for each distinct eigen decomposition)
num_subsets*num_transition_probs, // transition matrices (one for each node in each subset)
ngammacat, // rate categories
0, // scale buffers
NULL, // resource restrictions
0, // length of resource list
preferenceFlags, // preferred flags
requirementFlags, // required flags
&instance_details); // pointer for details
if (inst < 0) {
// beagleCreateInstance returns one of the following:
// valid instance (0, 1, 2, ...)
// error code (negative integer)
throw XStrom(boost::str(boost::format("Likelihood init function failed to create BeagleLib instance (BeagleLib error code was %d)") % _beagle_error[inst]));
}
InstanceInfo info;
info.handle = inst;
info.resourcenumber = instance_details.resourceNumber;
info.resourcename = instance_details.resourceName;
info.nstates = nstates;
info.nratecateg = ngammacat;
info.subsets = subset_indices;
info.npatterns = num_patterns;
info.partial_offset = num_internals;
info.tmatrix_offset = num_nodes;
_instances.push_back(info);
}
Note that beagleCreateInstance is a function defined by BeagleLib. Your program knows about it because you included the beagle.h header file at the top. The actual code for this function will not be stored in your program’s executable file; it will instead be loaded on demand from a Dynamic Link Library (provided by a file with a name that ends in .dll on Windows, .dylib on Mac, or .so in Unix) after your program begins to execute.
Calling beagleCreateInstance requires you to provide a lot of details. Here is a short description of these in the order in which they are supplied to the function:
Number of tips
This is the number of taxa in the tree.
Number of partials
This is the number of partials (also known as partials arrays or conditional likelihood arrays), and should equal the number of internal nodes plus the number of tips (if tip partials are being used) or the number of internal nodes (if tip states are being used).
Number of sequences
This is the number of observed sequences, which equals the number of taxa if we are using tip states or 0 if using tip partials.
Number of states
This is the number of states (e.g. 4 for DNA or RNA sequences, 20 for amino acid sequences, 61 for codons, etc.). Our program will only be using DNA sequences for now, so this value is set to 4. Note that because the number of states is fixed for any given instance, we will, eventually, need multiple BeagleLib instances to handle data subsets with different numbers of states.
Number of patterns
This is the number of unique data patterns (you will later tell BeagleLib how many sites have each pattern). In Figs. 10.1 and 10.2, the number of patterns is 3.
Number of models
This will be 1 if a single rate matrix and state frequencies are used for all sites (which is the case in the unpartitioned example shown in Fig. 10.1 above). If the data are partitioned and a different model is applied to each subset (as in Fig. 10.2), then the value specified here should equal the number of subsets.
Number of transition matrices
This is the number of transition matrices to be allocated, which equals the number of nodes in the tree if no partitioning is done. In the example shown in Fig. 10.1, there are 8 nodes and thus 8 transition probability matrices. In the partitioned example shown in Fig. 10.2, there are 8 nodes and 2 data subsets, which have different subset relative rates as well as different models, necessitating separate edge lengths and transition matrices. The number supplied in the partitioned example would be 2*8=16 (and note in Fig. 10.2 that the 16 transition matrices are indexed 0…15).
Number of rate categories
If your model allows for rate heterogeneity across sites, this is the number of rate categories. Use 1 if rates are assumed equal across sites (this is the case in the examples shown in both Fig. 10.1 and 10.2). Note that the number of rate categories applies to all data subsets. If you wish to apply a model with no rate heterogeneity to one subset and a 4-category discrete gamma rate heterogeneity model to a different subset, you will either need to create two separate instances (one specifying 1 rate category and the other specifying 4 rate categories), or you will need to specify 4 and simply use 4 categories with all four rates equal to 1 to handle the first subset.
Number of scale buffers
This has to do with scaling site likelihoods to avoid underflow, which is a concern for large trees, where site likelihoods can become so small that they cannot be distinguished them from zero given the number of bytes used to store the site likelihood value. The 0 value supplied here means we are not going to worry about scaling just yet.
Number of resource restrictions
This is a pointer to a list of potential resources (e.g. GPUs) on which this instance is allowed; we’ve supplied NULL (points to nothing) to indicate that we do not wish to restrict resources).
Length of resource list
The number of elements in the resource list supplied above (the pointer just points to the first element but stores no information about the total number of elements in the list, hence the need for this value); we’ve supplied 0 because we are not restricting BeagleLib.
Preferred flags
These tell BeagleLib your preferences (a key to possible flags is given below).
Required flags
These tell BeagleLib your requirements (a key to possible flags is given below).
Pointer for details
This is a pointer to a BeagleInstanceDetails structure, which will store details about implementation and resources (i.e. the decisions BeagleLib made given your preferences and requirements).
Here is the BeagleFlags enum in the beagle.h header file (this may change in a later version of BeagleLib, so consult the header file itself if you want to be sure to have the most accurate information for your version of BeagleLib):
*** NOTE: DO NOT ADD THIS TEXT TO YOUR PROGRAM ***
enum BeagleFlags {
BEAGLE_FLAG_PRECISION_SINGLE = 1 << 0, /* Single precision computation */
BEAGLE_FLAG_PRECISION_DOUBLE = 1 << 1, /* Double precision computation */
BEAGLE_FLAG_COMPUTATION_SYNCH = 1 << 2, /* Synchronous computation (blocking) */
BEAGLE_FLAG_COMPUTATION_ASYNCH = 1 << 3, /* Asynchronous computation (non-blocking) */
BEAGLE_FLAG_EIGEN_REAL = 1 << 4, /* Real eigenvalue computation */
BEAGLE_FLAG_EIGEN_COMPLEX = 1 << 5, /* Complex eigenvalue computation */
BEAGLE_FLAG_SCALING_MANUAL = 1 << 6, /* Manual scaling */
BEAGLE_FLAG_SCALING_AUTO = 1 << 7, /* Auto-scaling on (deprecated, may not work correctly) */
BEAGLE_FLAG_SCALING_ALWAYS = 1 << 8, /* Scale at every updatePartials (deprecated, may not work correctly) */
BEAGLE_FLAG_SCALING_DYNAMIC = 1 << 25, /* Manual scaling with dynamic checking (deprecated, may not work correctly) */
BEAGLE_FLAG_SCALERS_RAW = 1 << 9, /* Save raw scalers */
BEAGLE_FLAG_SCALERS_LOG = 1 << 10, /* Save log scalers */
BEAGLE_FLAG_INVEVEC_STANDARD = 1 << 20, /* Inverse eigen vectors passed to BEAGLE have not been transposed */
BEAGLE_FLAG_INVEVEC_TRANSPOSED = 1 << 21, /* Inverse eigen vectors passed to BEAGLE have been transposed */
BEAGLE_FLAG_VECTOR_SSE = 1 << 11, /* SSE computation */
BEAGLE_FLAG_VECTOR_AVX = 1 << 24, /* AVX computation */
BEAGLE_FLAG_VECTOR_NONE = 1 << 12, /* No vector computation */
BEAGLE_FLAG_THREADING_OPENMP = 1 << 13, /* OpenMP threading */
BEAGLE_FLAG_THREADING_NONE = 1 << 14, /* No threading */
BEAGLE_FLAG_PROCESSOR_CPU = 1 << 15, /* Use CPU as main processor */
BEAGLE_FLAG_PROCESSOR_GPU = 1 << 16, /* Use GPU as main processor */
BEAGLE_FLAG_PROCESSOR_FPGA = 1 << 17, /* Use FPGA as main processor */
BEAGLE_FLAG_PROCESSOR_CELL = 1 << 18, /* Use Cell as main processor */
BEAGLE_FLAG_PROCESSOR_PHI = 1 << 19, /* Use Intel Phi as main processor */
BEAGLE_FLAG_PROCESSOR_OTHER = 1 << 26, /* Use other type of processor */
BEAGLE_FLAG_FRAMEWORK_CUDA = 1 << 22, /* Use CUDA implementation with GPU resources */
BEAGLE_FLAG_FRAMEWORK_OPENCL = 1 << 23, /* Use OpenCL implementation with GPU resources */
BEAGLE_FLAG_FRAMEWORK_CPU = 1 << 27 /* Use CPU implementation */
};
The setTipStates member function
This function is called in initBeagleLib if _ambiguity_equals_missing is true. It provides BeagleLib with the observed data for each leaf node in the tree. The data are stored in a Data object and made available to the function by means of the shared pointer data member _data. By the time these data are used, BeagleLib will know the length of this array of states (it is provided in the beagleCreateInstance function that was called in the newInstance member function above). Note that this function assumes that all necessary BeagleLib instances have already been created.
inline void Likelihood::setTipStates() {
assert(_instances.size() > 0);
assert(_data);
Data::state_t one = 1;
for (auto & info : _instances) {
std::vector<int> states(info.nstates*info.npatterns);
// Loop through all rows of the data matrix, setting the tip states for one taxon each row
unsigned t = 0;
for (auto & row : _data->getDataMatrix()) {
// Loop through all subsets assigned to this instance
unsigned k = 0;
for (unsigned s : info.subsets) {
// Loop through all patterns in this subset
auto interval = _data->getSubsetBeginEnd(s);
for (unsigned p = interval.first; p < interval.second; p++) {
// d is the state for taxon t, pattern p (in subset s)
// d is stored as a bit field (e.g., for nucleotide data, A=1, C=2, G=4, T=8, ?=15),
// but BeagleLib expects states to be integers (e.g. for nucleotide data,
// A=0, C=1, G=2, T=3, ?=4).
Data::state_t d = row[p];
// Handle common nucleotide case separately
if (info.nstates == 4) {
if (d == 1)
states[k++] = 0;
else if (d == 2)
states[k++] = 1;
else if (d == 4)
states[k++] = 2;
else if (d == 8)
states[k++] = 3;
else
states[k++] = 4;
}
else {
// This case is for any other data type except nucleotide
int s = -1;
for (unsigned b = 0; b < info.nstates; b++) {
if (d == one << b) {
s = b;
break;
}
}
if (s == -1)
states[k++] = info.nstates;
else
states[k++] = s;
}
} // pattern loop
} // subset loop
int code = beagleSetTipStates(
info.handle, // Instance number
t, // Index of destination compactBuffer
&states[0]); // Pointer to compact states vector
if (code != 0)
throw XStrom(boost::format("failed to set tip state for taxon %d (\"%s\"; BeagleLib error code was %d)") % (t+1) % _data->getTaxonNames()[t] % code % _beagle_error[code]);
++t;
}
}
}
The setTipPartials member function
This function is called in initBeagleLib if _ambiguity_equals_missing is false. It provides BeagleLib with the observed data for each leaf node in the tree in the form of partials arrays (as in the examples from figures 10.1 and 10.2). Using partials to store tip states requires more memory and comes with a substantial computation cost as well because this essentially doubles the number of loops over states needed in calculating the likelihood. Hence, we will give users the option (via _ambiguity_equals_missing) to treat all ambiguous states as fully missing if they wish to eliminate the additional computational burden associated with correctly handling ambiguities.
As in setTipStates, the data are stored in a Data object and made available to the function by means of the shared pointer data member _data. Note that this function also assumes that all necessary BeagleLib instances have already been created.
inline void Likelihood::setTipPartials() {
assert(_instances.size() > 0);
assert(_data);
Data::state_t one = 1;
for (auto & info : _instances) {
if (info.nstates != 4)
throw XStrom(boost::format("This program can handle only 4-state DNA/RNA data. You specified data having %d states for at least one data subset.") % info.nstates);
std::vector<double> partials(info.nstates*info.npatterns);
// Loop through all rows of data matrix, setting the tip states for one taxon each row
unsigned t = 0;
for (auto & row : _data->getDataMatrix()) {
// Loop through all subsets assigned to this instance
unsigned k = 0;
for (unsigned s : info.subsets) {
// Loop through all patterns in this subset
auto interval = _data->getSubsetBeginEnd(s);
for (unsigned p = interval.first; p < interval.second; p++) {
// d is the state for taxon t, pattern p (in subset s)
Data::state_t d = row[p];
// Handle common nucleotide case separately
if (info.nstates == 4) {
partials[k++] = d & 1 ? 1.0 : 0.0;
partials[k++] = d & 2 ? 1.0 : 0.0;
partials[k++] = d & 4 ? 1.0 : 0.0;
partials[k++] = d & 8 ? 1.0 : 0.0;
}
else {
// This case is for any other data type except nucleotide
for (unsigned b = 0; b < info.nstates; b++) {
partials[k++] = d & (one << b) ? 1.0 : 0.0;
}
}
}
}
int code = beagleSetTipPartials(
info.handle, // Instance number
t, // Index of destination compactBuffer
&partials[0]); // Pointer to compact states vector
if (code != 0)
throw XStrom(boost::format("failed to set tip state for taxon %d (\"%s\"; BeagleLib error code was %d)") % (t+1) % _data->getTaxonNames()[t] % code % _beagle_error[code]);
++t;
}
}
}
In the examples shown in Figures 10.1 and 10.2, the original data set had 8 sites, compressed into just 3 patterns. (Yes, this is way smaller than any real data set, but having only 3 patterns allows me to show you complete leaf partials arrays!) The 3 site patterns are stored in the data_matrix retrieved from the Data object using the function call _data->getDataMatrix(). Each of the 3 states stored for each leaf requires _nstates=4 floating point values, which explains why the vector partials defined at the top of this function has length _states*_npatterns.
Consider the case of the second pattern in taxon 3, which has an ambiguous state Y that could be either a C or a T (i.e. either pyrimidine). The four floating point partial likelihoods used to store this information are 0.0, 1.0, 0.0, 1.0. The first and third values (both 0.0) correspond to A and G, respectively, while the second and fourth values (both 1.0) correspond to C and T.
The four partials corresponding to one state are set in these four lines:
partials[k++] = d & 1 ? 1.0 : 0.0;
partials[k++] = d & 2 ? 1.0 : 0.0;
partials[k++] = d & 4 ? 1.0 : 0.0;
partials[k++] = d & 8 ? 1.0 : 0.0;
You have to think in binary in order to make sense of these lines. The variable d holds a leaf state, which may be a combination of states (as for the pyrimidine ambiguity example above). The d & 1, d & 2, d & 4 and d & 8 expressions test, respectively, whether the state code d includes A (1), C (2), G (4) or T (8). For the pyrimidine example, the state code d would equal 2+8=10, which is 1010 in binary. The tests performed in these four lines are illustrated below:
test for A test for C test for G test for T
d 1010 d 1010 d 1010 d 1010
1 0001 2 0010 4 0100 8 1000
---------- ---------- ---------- ----------
d & 1 0000 d & 2 0010 d & 4 0000 d & 8 1000
Thus, the tests for C and T both result in true values (anything except 0) while the tests for A and G result in false value (both are 0000 because no 1 bits are in common).
The best way to think about the meaning of these partial likelihood values is to imagine a point (X) immediately below the leaf Y (zero branch length separates X from Y). The four values 0.0, 1.0, 0.0, and 1.0, correspond to the probabilities of the state at Y given the state at X. The first 0.0 corresponds to state A at X and says that the probability of seeing a pyrimidine at Y given that there is an A at point X is 0.0 (because the zero branch length means there is no chance that the A at X could change into either a C or T at Y). The second 1.0 value corresponds to state C at X and says that the probability of seeing a pyrimidine at Y is 1.0 (certain) because there is already a pyrimidine at X and the zero branch length between X and Y means this pyrimidine cannot change to anything else.
Partial likelihood arrays will also be calculated at internal nodes of the tree. For an internal node, each cell in the partials vector holds the likelihood (probability of all observed data) above that node in the tree given one particular state at that internal node. These internal node partials can be something other than 0.0 or 1.0 because there is length > 0 associated with the edges in the subtree rooted at that internal node.
The setPatternPartitionAssignments member function
This function specifies the subset to which every pattern belongs. The only tricky part is that there may be several BeagleLib instances, and BeagleLib wants pattern and subset indices to be relative to a particular instance.
For example, suppose there are 3 data subsets, and the first (index 0) and third (index 2) are in instance 0 and contain 5 and 6 patterns, respectively, while the second (index 1) is in a separate instance 1 and has 7 patterns. If these are the actual subset and pattern indices,
subset | <----- 0 -----> | <-------- 1 ---------> | <--------- 2 -------> |
pattern | 0 1 2 3 4 | 6 7 8 9 10 11 12 | 15 16 17 18 19 20|
then these are the indices BeagleLib wants for each instance:
Instance 0:
subset | <---- 0 -----> | <----- 1 -----> |
pattern | 0 1 2 3 4 | 0 1 2 3 4 5|
Instance 1:
subset | <------- 0 -------> |
pattern | 0 1 2 3 4 5 6 |
The vector v is resized for each instance to hold the (relative) subset index for each pattern. Once this vector is filled, it is passed to BeagleLib via the beagleSetPatternPartitions function. For the example above, the vector v would look like this for the 2 instances:
Instance 0:
v | 0 0 0 0 0 1 1 1 1 1 1|
Instance 1:
v | 0 0 0 0 0 0 0 |
Here is the body of the function:
inline void Likelihood::setPatternPartitionAssignments() {
assert(_instances.size() > 0);
assert(_data);
// beagleSetPatternPartitions does not need to be called if data are unpartitioned
// (and, in fact, BeagleLib only supports partitioning for 4-state instances if GPU is used,
// so not calling beagleSetPatternPartitions allows unpartitioned codon model analyses)
if (_instances.size() == 1 && _instances[0].subsets.size() == 1)
return;
Data::partition_key_t v;
// Loop through all instances
for (auto & info : _instances) {
unsigned nsubsets = (unsigned)info.subsets.size();
v.resize(info.npatterns);
unsigned pattern_index = 0;
// Loop through all subsets assigned to this instance
unsigned instance_specific_subset_index = 0;
for (unsigned s : info.subsets) {
// Loop through all patterns in this subset
auto interval = _data->getSubsetBeginEnd(s);
for (unsigned p = interval.first; p < interval.second; p++) {
v[pattern_index++] = instance_specific_subset_index;
}
++instance_specific_subset_index;
}
int code = beagleSetPatternPartitions(
info.handle, // instance number
nsubsets, // number of data subsets (equals 1 if data are unpartitioned)
&v[0]); // vector of subset indices: v[i] = 0 means pattern i is in subset 0
if (code != 0) {
throw XStrom(boost::format("failed to set pattern partition. BeagleLib error code was %d (%s)") % code % _beagle_error[code]);
}
}
}
The setPatternWeights member function
Before computing a likelihood, BeagleLib will need to know how many sites exhibited each site pattern in the data set: that is, the pattern counts. In the examples shown in Figures 10.1 and 10.2, there are 3 patterns and the counts are 2, 1, 5. Some patterns will be found at a single site, whereas other patterns will be common to many sites (for example, constant patterns in which the same state is found for all taxa are relatively common). The Data class stores a vector of site counts for each pattern in its _pattern_counts data member, so all we have to do here is transfer those counts to our BeagleLib instance. Note that this function assumes that all necessary BeagleLib instances have already been created.
inline void Likelihood::setPatternWeights() {
assert(_instances.size() > 0);
assert(_data);
Data::pattern_counts_t v;
auto pattern_counts = _data->getPatternCounts();
assert(pattern_counts.size() > 0);
// Loop through all instances
for (auto & info : _instances) {
v.resize(info.npatterns);
unsigned pattern_index = 0;
// Loop through all subsets assigned to this instance
for (unsigned s : info.subsets) {
// Loop through all patterns in this subset
auto interval = _data->getSubsetBeginEnd(s);
for (unsigned p = interval.first; p < interval.second; p++) {
v[pattern_index++] = pattern_counts[p];
}
}
int code = beagleSetPatternWeights(
info.handle, // instance number
&v[0]); // vector of pattern counts: v[i] = 123 means pattern i was encountered 123 times
if (code != 0)
throw XStrom(boost::format("Failed to set pattern weights for instance %d. BeagleLib error code was %d (%s)") % info.handle % code % _beagle_error[code]);
}
}
The setAmongSiteRateHeterogenetity member function
BeagleLib handles rate heterogeneity in a very general way (as it handles all aspects of models). It expects you to provide it with an array of relative substitution rates and a corresponding array of rate probabilities. It does not care how you got these two arrays, so both rates and probabilities can be completely arbitrary (subject to certain constraints: probabilities must add to 1 and relative rates must have mean 1), but in this tutorial we will ultimately supply BeagleLib with rates and probabilities derived from the proportion of variable sites and discrete Gamma distribution widely used for modeling among-site rate heterogeneity.
This function calls two BeagleLib functions, beagleSetCategoryRates (or beagleSetCategoryRatesWithIndex) and beagleSetCategoryWeights, both of which assume that a valid BeagleLib instance exists. For equal rates, the relative rate for each site is 1.0 and the probability that each site has that relative rate is also 1.0, so the rates and probs arrays passed to BeagleLib both have a single element that has value 1.0. This is the case shown in the examples illustrated by both Fig. 10.1 and Fig. 10.2.
inline void Likelihood::setAmongSiteRateHeterogenetity() {
assert(_instances.size() > 0);
int code = 0;
// For now we are assuming rates among sites are equal
double rates[1] = {1.0};
double probs[1] = {1.0};
// Loop through all instances
for (auto & info : _instances) {
// Loop through all subsets assigned to this instance
for (unsigned instance_specific_subset_index = 0; instance_specific_subset_index < info.subsets.size(); instance_specific_subset_index++) {
code = beagleSetCategoryRatesWithIndex(
info.handle, // instance number
instance_specific_subset_index, // subset index
rates); // vector containing rate scalers
if (code != 0)
throw XStrom(boost::str(boost::format("Failed to set category rates for BeagleLib instance %d. BeagleLib error code was %d (%s)") % info.handle % code % _beagle_error[code]));
code = beagleSetCategoryWeights(
info.handle, // Instance number
instance_specific_subset_index, // Index of category weights buffer
probs); // Category weights array (categoryCount)
if (code != 0)
throw XStrom(boost::str(boost::format("Failed to set category probabilities for BeagleLib instance %d. BeagleLib error code was %d (%s)") % info.handle % code % _beagle_error[code]));
}
}
}
Note that while beagleSetCategoryRates may be used to set rates in the unpartitioned case, we use beagleSetCategoryRatesWithIndex here just in case our data are partitioned: the index in the name of the function refers to the index (relative to the instance) of the data subset to which these rates will be applied. This allows, for example, a different gamma shape parameter to be used for each subset if a discrete gamma distribution is being used to model among-site rate heterogeneity.
The setModelRateMatrix member function
BeagleLib handles the specification of a substitution model in a very general way. Specifically, it requires you to provide the equilibrium state frequencies and the eigenvalues and eigenvectors (and inverse eigenvectors) of the instantaneous rate matrix. We will be using the simplest model (the Jukes-Cantor, or JC69, model), which specifies equal base frequencies and a rate matrix in which all off-diagonal rates are identical. The BeagleLib function beagleSetStateFrequencies is used to transfer the state frequencies, and the function beagleSetEigenDecomposition is used to transfer the eigenvalues, eigenvectors, and inverse eigenvectors (all in the form of flat, single-dimensional arrays), to an existing BeagleLib instance. You may wonder why even simple models such as JC69, for which closed-form expressions (i.e. formulas) are available for transition probabilities, must be specified as eigensystems. The answer is that most models (e.g. GTR) used these days in phylogenetics are complex enough that transition probabilities must be computed by diagonalizing the rate matrix, so the approach used by BeagleLib is straightforward, flexible enough to allow quite complex models of evolution, and yet as simple as possible given the need to maintain generality. Don’t worry, the tutorial will later use the Eigen library to compute eigensystems for models - you will not need to hard code eigenvalue and eigenvectors for all models!
inline void Likelihood::setModelRateMatrix() {
assert(_instances.size() > 0);
int code = 0;
double state_freqs[4] = {0.25, 0.25, 0.25, 0.25};
double eigenvalues[4] = {
-4.0/3.0,
-4.0/3.0,
-4.0/3.0,
0.0
};
double eigenvectors[16] = {
-1, -1, -1, 1,
0, 0, 1, 1,
0, 1, 0, 1,
1, 0, 0, 1
};
double inverse_eigenvectors[16] = {
-0.25, -0.25, -0.25, 0.75,
-0.25, -0.25, 0.75, -0.25,
-0.25, 0.75, -0.25, -0.25,
0.25, 0.25, 0.25, 0.25
};
// Loop through all instances
for (auto & info : _instances) {
// Loop through all subsets assigned to this instance
for (unsigned instance_specific_subset_index = 0; instance_specific_subset_index < info.subsets.size(); instance_specific_subset_index++) {
code = beagleSetStateFrequencies(
info.handle, // Instance number
instance_specific_subset_index, // Index of state frequencies buffer
state_freqs); // State frequencies array (stateCount)
if (code != 0)
throw XStrom(boost::str(boost::format("Failed to set state frequencies for BeagleLib instance %d. BeagleLib error code was %d (%s)") % info.handle % code % _beagle_error[code]));
code = beagleSetEigenDecomposition(
info.handle, // Instance number
instance_specific_subset_index, // Index of eigen-decomposition buffer
(const double *)eigenvectors, // Flattened matrix (stateCount x stateCount) of eigenvectors
(const double *)inverse_eigenvectors, // Flattened matrix (stateCount x stateCount) of inverse-eigenvectors
eigenvalues); // Vector of eigenvalues
if (code != 0)
throw XStrom(boost::str(boost::format("Failed to set eigen decomposition for BeagleLib instance %d. BeagleLib error code was %d (%s)") % info.handle % code % _beagle_error[code]));
}
}
}
The defineOperations member function
BeagleLib does not define or use trees per se. Instead, we must tell BeagleLib exactly which transition matrices to compute and which partial likelihoods to calculate in order to compute the likelihood. To do this, we traverse a tree (passed in using the shared pointer t to a Tree object) in reverse level-order sequence (i.e. visiting all descendants of an upper level before visiting any of the nodes at the next lower level) and create a list of “operations” for BeagleLib to carry out. We could visit nodes in postorder sequence (by visiting the _preorder vector in reverse order), but that would be less efficient (as explained earlier in the tutorial when we created the _preorder and _levelorder vectors) because all nodes at a given level can be calculated at the same time, yet postorder sequence makes us wait for some of these until dependent nodes at lower levels are finished.
While we are traversing the tree, we will create a vector of node numbers (stored in the data member _pmatrix_index) and edge lengths (_edge_lengths) as they are encountered for use in the calcLogLikelihood function defined below. We will also precalculate _eigen_indices and _category_rate_indices, which are used in updateTransitionMatrices. These are all std::map variables with keys equal to the instance handle and value equal to a std::vector (of int except for _edge_lengths, which is a double-valued vector). These 4 vectors, along with _operations, are initialized (for every BeagleLib instance) near the beginning of the defineOperations function.
The member function queueTMatrixRecalculation handles additions to _pmatrix_index, _edge_lengths, _eigen_indices, and _category_rate_indices, while the member function queuePartialsRecalculation is used to create the entries that will be added to the _operations vector. I will discuss these two queuing functions next.
Here is the body of the defineOperations member function:
inline void Likelihood::defineOperations(Tree::SharedPtr t) {
assert(_instances.size() > 0);
assert(t);
assert(t->isRooted() == _rooted);
_relrate_normalizing_constant = 1.0; // assuming subset rates all 1.0 for now
// Start with a clean slate
for (auto & info : _instances) {
_operations[info.handle].clear();
_pmatrix_index[info.handle].clear();
_edge_lengths[info.handle].clear();
_eigen_indices[info.handle].clear();
_category_rate_indices[info.handle].clear();
}
// Loop through all nodes in reverse level order
for (auto nd : boost::adaptors::reverse(t->_levelorder)) {
assert(nd->_number >= 0);
if (!nd->_left_child) {
// This is a leaf
queueTMatrixRecalculation(nd);
}
else {
// This is an internal node
queueTMatrixRecalculation(nd);
// Internal nodes have partials to be calculated, so define
// an operation to compute the partials for this node
Node * lchild = nd->_left_child;
assert(lchild);
Node * rchild = lchild->_right_sib;
assert(rchild);
queuePartialsRecalculation(nd, lchild, rchild);
}
}
}
The queueTMatrixRecalculation member function
The updateTransitionMatrices function (discussed below) will update all the transition matrices needed to compute the likelihood, but it requires, at the very least, a vector of edge lengths (_edge_lengths) and a vector of transition matrix indices (_pmatrix_index) for each instance. In addition, if the instance has more than one subset, updateTransitionMatrices also requires a vectors of eigensystem indices (_eigen_indices) and a vector of among-site rate heterogeneity indices (_category_rate_indices). This function adds to all of these vectors, essentially queuing up a recalculation of all transition matrices associated with the Node object passed in as nd.
The function involves looping over every instance and, within each instance, all subsets. The index of a particular transition matrix depends on the index of the node as well as the subset index, and the function getTMatrixIndex calculates that for us.
Different subsets can have different relative rates of substitution, but, initially, we will assume that all subsets evolve at the same relative rate (1.0).
inline void Likelihood::queueTMatrixRecalculation(Node * nd) {
double subset_relative_rate = 1.0; // assuming all subsets have equal relative rates for now
for (auto & info : _instances) {
unsigned instance_specific_subset_index = 0;
for (unsigned s : info.subsets) {
unsigned tindex = getTMatrixIndex(nd, info, instance_specific_subset_index);
_pmatrix_index[info.handle].push_back(tindex);
_edge_lengths[info.handle].push_back(nd->_edge_length*subset_relative_rate);
_eigen_indices[info.handle].push_back(s);
_category_rate_indices[info.handle].push_back(s);
++instance_specific_subset_index;
}
}
}
The queuePartialsRecalculation member function
This function adds an entry to the _operations vector for each BeagleLib instance. It calls another helper function, addOperation, to add each operation.
inline void Likelihood::queuePartialsRecalculation(Node * nd, Node * lchild, Node * rchild) {
for (auto & info : _instances) {
unsigned instance_specific_subset_index = 0;
for (unsigned s : info.subsets) {
addOperation(info, nd, lchild, rchild, instance_specific_subset_index);
++instance_specific_subset_index;
}
}
}
The addOperation member function
The operations are provided to BeagleLib as a single-dimension (flat) vector. If 3 operations are defined for a particular BeagleLib instance, the _operations vector for that instance will be comprise 21 elements (for the simplest case of unpartitioned data).
Important! When I say unpartitioned in the context of defining operations, what I really mean is single data subset for a given BeagleLib instance. If each subset of your partition is assigned to a different BeagleLib instance (because they all have a distinct combination of number of states and number of rate categories), then each instance still considers the data to be unpartitioned because the instances “sees” only the single data subset assigned to it.
Each operation is defined by providing 7 (unpartitioned data) or 9 (if data is partitioned) values in a particular sequence for each internal node.
Here is a description of these values:
Destination partials
The index of the internal node (leaf nodes are indexed from
0,...,n-1, and internal nodes are indexed starting atn, which is the number of taxa). This value tells BeagleLib which partial (conditional likelihood array) to compute.
Destination scale write
We provide the value
BEAGLE_OP_NONEto indicate we are not scaling site likelihoods.
Destination scale read
We provide the value
BEAGLE_OP_NONEto indicate we are not scaling site likelihoods.
Left child partials
The index of the left child node.
Left child transition matrix
The index of the left child node. This tells BeagleLib which transition matrix to use to accommodate evolution along the edge leading to the left child.
Right child partials
The index of the right child node.
Right child transition matrix
The index of the right child node. This tells BeagleLib which transition matrix to use to accommodate evolution along the edge leading to the right child.
Subset index
The index of the subset. This is the first of two values only supplied if data are partitioned.
Cumulative scale index
This is the second of the two values only used if data are partitioned. We provide the value
BEAGLE_OP_NONEto indicate we are not scaling site likelihoods.
inline void Likelihood::addOperation(InstanceInfo & info, Node * nd, Node * lchild, Node * rchild, unsigned subset_index) {
assert(nd);
assert(lchild);
assert(rchild);
// 1. destination partial to be calculated
int partial_dest = getPartialIndex(nd, info);
_operations[info.handle].push_back(partial_dest);
// 2. destination scaling buffer index to write to
int scaler_index = getScalerIndex(nd, info);
_operations[info.handle].push_back(scaler_index);
// 3. destination scaling buffer index to read from
_operations[info.handle].push_back(BEAGLE_OP_NONE);
// 4. left child partial index
int partial_lchild = getPartialIndex(lchild, info);
_operations[info.handle].push_back(partial_lchild);
// 5. left child transition matrix index
unsigned tindex_lchild = getTMatrixIndex(lchild, info, subset_index);
_operations[info.handle].push_back(tindex_lchild);
// 6. right child partial index
int partial_rchild = getPartialIndex(rchild, info);
_operations[info.handle].push_back(partial_rchild);
// 7. right child transition matrix index
unsigned tindex_rchild = getTMatrixIndex(rchild, info, subset_index);
_operations[info.handle].push_back(tindex_rchild);
if (info.subsets.size() > 1) {
// 8. index of partition subset
_operations[info.handle].push_back(subset_index);
// 9. cumulative scale index
_operations[info.handle].push_back(BEAGLE_OP_NONE);
}
}
Summary of operations for unpartitioned and partitioned examples
In the 5-taxon example illustrated in Fig. 10.1 above, there are 3 internal partial arrays that need to be calculated and the data are unpartitioned, so the operations array will comprise 3*7=21 values. Here are the 21 values corresponding to the example shown in Fig. 10.1:
index value description
-------------------------------------------------------
0 5 destination partials
1 BEAGLE_OP_NONE destination scale write
2 BEAGLE_OP_NONE destination scale read
3 4 left child partials
4 4 left child transition matrix
5 2 right child partials
6 2 right child transition matrix
7 6 destination partials
8 BEAGLE_OP_NONE destination scale write
9 BEAGLE_OP_NONE destination scale read
10 1 left child partials
11 1 left child transition matrix
12 5 right child partials
13 5 right child transition matrix
14 7 destination partials
15 BEAGLE_OP_NONE destination scale write
16 BEAGLE_OP_NONE destination scale read
17 6 left child partials
18 6 left child transition matrix
19 3 right child partials
20 3 right child transition matrix
In the 5-taxon partitioned example illustrated in Fig. 10.2 above, there are 3 internal partial arrays that need to be calculated, but the data are partitioned with 2 subsets, so the operations array will comprise 3*2*9=54 values. Here are the 54 values corresponding to the example shown in Fig. 10.2:
index value description
-------------------------------------------------------
0 5 destination partials
1 BEAGLE_OP_NONE destination scale write
2 BEAGLE_OP_NONE destination scale read
3 4 left child partials
4 4 left child transition matrix
5 2 right child partials
6 2 right child transition matrix
7 0 subset index
8 BEAGLE_OP_NONE index of scaleBuffer to store accumulated factors
9 5 destination partials
10 BEAGLE_OP_NONE destination scale write
11 BEAGLE_OP_NONE destination scale read
12 4 left child partials
13 12 left child transition matrix
14 2 right child partials
15 10 right child transition matrix
16 1 subset index
17 BEAGLE_OP_NONE index of scaleBuffer to store accumulated factors
18 6 destination partials
19 BEAGLE_OP_NONE destination scale write
20 BEAGLE_OP_NONE destination scale read
21 1 left child partials
22 1 left child transition matrix
23 5 right child partials
24 5 right child transition matrix
25 0 subset index
26 BEAGLE_OP_NONE index of scaleBuffer to store accumulated factors
27 6 destination partials
28 BEAGLE_OP_NONE destination scale write
29 BEAGLE_OP_NONE destination scale read
30 1 left child partials
31 9 left child transition matrix
32 5 right child partials
33 13 right child transition matrix
34 1 subset index
35 BEAGLE_OP_NONE index of scaleBuffer to store accumulated factors
36 7 destination partials
37 BEAGLE_OP_NONE destination scale write
38 BEAGLE_OP_NONE destination scale read
39 6 left child partials
40 6 left child transition matrix
41 3 right child partials
42 3 right child transition matrix
43 0 subset index
44 BEAGLE_OP_NONE index of scaleBuffer to store accumulated factors
45 7 destination partials
46 BEAGLE_OP_NONE destination scale write
47 BEAGLE_OP_NONE destination scale read
48 6 left child partials
49 14 left child transition matrix
50 3 right child partials
51 11 right child transition matrix
52 1 subset index
53 BEAGLE_OP_NONE index of scaleBuffer to store accumulated factors
The getPartialIndex member function
This function returns the index of a particular partials buffer, which is simply the node number. You may wonder why we have invented a member function just to return the node number. The answer is that determining the partials index will become more complex later steps in the tutorial, and creating this function now means that we will need only to update this function later rather than change all the places that call getPartialIndex.
inline unsigned Likelihood::getPartialIndex(Node * nd, InstanceInfo & info) const {
// Note: do not be tempted to subtract _ntaxa from pindex: BeagleLib does this itself
assert(nd->_number >= 0);
return nd->_number;
}
The getTMatrixIndex member function
This function returns the index of a particular transition probability matrix buffer. This index will be simply the node number if the instance is managing only one subset. If the instance manages more than one subsets, then the subset index is needed in the calculation of the index.
inline unsigned Likelihood::getTMatrixIndex(Node * nd, InstanceInfo & info, unsigned subset_index) const {
unsigned tindex = subset_index*info.tmatrix_offset + nd->_number;
return tindex;
}
The getScalerIndex member function
This function returns the index of the buffer holding scalers for each pattern for node nd in the specified BeagleLib instance. For now, because we are not correcting for underflow and thus not using scalers, just return BEAGLE_OP_NONE.
inline unsigned Likelihood::getScalerIndex(Node * nd, InstanceInfo & info) const {
return BEAGLE_OP_NONE;
}
The updateTransitionMatrices member function
This function recalculates all transition matrices. In the queueTMatrixRecalculation member function, we built a vector (_pmatrix_index) for each instance containing the indices of all nodes that have a transition matrix needing to be recomputed, and we also created instance-specific vectors of _edge_lengths containing the edge lengths corresponding to the nodes listed in _pmatrix_index, so here all we need do is provide these lists to BeagleLib. The queueTMatrixRecalculation member function also built up _eigen_indices and _category_rate_indices vectors if the instance manages more than one subset.
There are two functions in BeagleLib that are concerned with updating transition matrices: beagleUpdateTransitionMatrices and beagleUpdateTransitionMatricesWithMultipleModels. The function beagleUpdateTransitionMatrices is used when not partitioning, while beagleUpdateTransitionMatricesWithMultipleModels is used when partitioning. Again, partitioning is considered on an individual instance basis: if data are partitioned, but a particular instance only deals with one data subset, then, from the perspective of that instance, the data are unpartitioned and beagleUpdateTransitionMatrices would be used, not beagleUpdateTransitionMatricesWithMultipleModels.
For beagleUpdateTransitionMatrices (unpartitioned case), the first argument must be a valid BeagleLib instance, the second argument is the index of the eigen decomposition to use (0 in our case because there is only one), the third argument is the address of the first element of the array of node indices specifying the transition matrices to be computed, the fourth and fifth arguments are NULL because we are not concerned with calculating first and second deriviatives, the sixth argument is the address of the first element of the array of edge lengths, and the seventh and final argument is the number of transition probabilities to calculate.
The values of the arrays _pmatrix_index, and _edge_lengths that would be supplied to the beagleUpdateTransitionMatrices function for the example shown in Fig. 10.1 are given below. Note that the values are in reverse level order sequence.
index _pmatrix_index _edge_lengths
------------------------------------
0 3 0.38
1 2 0.11
2 4 0.10
3 1 0.23
4 5 0.12
5 6 0.13
6 7 0.15
The beagleUpdateTransitionMatricesWithMultipleModels (partitioned case) has a similar list of arguments, with the exception that _eigen_indices and _category_rate_indices vectors are supplied to provide values for each subset.
The corresponding arrays for the partitioned example shown in Fig. 10.2 are given below.
index _pmatrix_index _edge_lengths _eigen_indices _category_rate_indices
-------------------------------------------------------------------------
0 3 0.950 0 0
1 11 0.038 1 1
2 2 0.275 0 0
3 10 0.011 1 1
4 4 0.250 0 0
5 12 0.010 1 1
6 1 0.575 0 0
7 9 0.023 1 1
8 5 0.300 0 0
9 13 0.012 1 1
10 6 0.325 0 0
11 14 0.013 1 1
12 7 0.375 0 0
13 15 0.015 1 1
You may be puzzled why thee are two sets of rates and probabilities, one for each subset, when the number of rate categories is 1 for this example. After all, the rates and probabilities must both be 1 in this case, so why duplicate the storage? The answer is that it is not necessary, but, to keep things simple, the tutorial will always allocate a separate set of rates and probs for each subset. For simple cases like this it is indeed wasteful, so you were correct in being puzzled.
Here is the body of the updateTransitionMatrices member function:
inline void Likelihood::updateTransitionMatrices() {
assert(_instances.size() > 0);
if (_pmatrix_index.size() == 0)
return;
// Loop through all instances
for (auto & info : _instances) {
int code = 0;
unsigned nsubsets = (unsigned)info.subsets.size();
if (nsubsets > 1) {
code = beagleUpdateTransitionMatricesWithMultipleModels(
info.handle, // Instance number
&_eigen_indices[info.handle][0], // Index of eigen-decomposition buffer
&_category_rate_indices[info.handle][0], // category rate indices
&_pmatrix_index[info.handle][0], // transition probability matrices to update
NULL, // first derivative matrices to update
NULL, // second derivative matrices to update
&_edge_lengths[info.handle][0], // List of edge lengths
(int)_pmatrix_index[info.handle].size()); // Length of lists
}
else {
code = beagleUpdateTransitionMatrices(
info.handle, // Instance number
0, // Index of eigen-decomposition buffer
&_pmatrix_index[info.handle][0], // transition probability matrices to update
NULL, // first derivative matrices to update
NULL, // second derivative matrices to update
&_edge_lengths[info.handle][0], // List of edge lengths
(int)_pmatrix_index[info.handle].size()); // Length of lists
}
if (code != 0)
throw XStrom(boost::str(boost::format("Failed to update transition matrices for instance %d. BeagleLib error code was %d (%s)") % info.handle % code % _beagle_error[code]));
}
}
The calculatePartials member function
This function instructs BeagleLib to update all its partials using the information in the operations array. In the defineOperations member function, we created instance-specific vectors storing all the information BeagleLib needs, so here we simply allow it to copy these vectors stored in the _operations map.
Once again, BeagleLib considers data to be partitioned if there is more than one subset attached to a particular instance. In this case, we use the BeagleLib function beagleUpdatePartialsByPartition to carry out the update. For unpartitioned data (instances in which only one data subset is attached), we use the beagleUpdatePartials BeagleLib function.
The first argument of either of these functions must be a valid BeagleLib instance, the second argument is the address of the starting element of the appropriate vector stored in _operations, the third argument is the number of elements in this operations vector, and the final argument (beagleUpdatePartials only) is the index of the scale buffer used to store accumulated scaling factors, but because we are not scaling site likelihoods currently, we supply the value BEAGLE_OP_NONE.
inline void Likelihood::calculatePartials() {
assert(_instances.size() > 0);
if (_operations.size() == 0)
return;
int code = 0;
// Loop through all instances
for (auto & info : _instances) {
unsigned nsubsets = (unsigned)info.subsets.size();
if (nsubsets > 1) {
code = beagleUpdatePartialsByPartition(
info.handle, // Instance number
(BeagleOperationByPartition *) &_operations[info.handle][0], // BeagleOperation list specifying operations
(int)(_operations[info.handle].size()/9)); // Number of operations
if (code != 0)
throw XStrom(boost::format("failed to update partials. BeagleLib error code was %d (%s)") % code % _beagle_error[code]);
}
else {
// no partitioning, just one data subset
code = beagleUpdatePartials(
info.handle, // Instance number
(BeagleOperation *) &_operations[info.handle][0], // BeagleOperation list specifying operations
(int)(_operations[info.handle].size()/7), // Number of operations
BEAGLE_OP_NONE); // Index number of scaleBuffer to store accumulated factors
if (code != 0)
throw XStrom(boost::format("failed to update partials. BeagleLib error code was %d (%s)") % code % _beagle_error[code]);
}
}
}
The calcInstanceLogLikelihood member function
This member function does the work of computing the log-likelihood for just the data managed by a single BeagleLib instance. The calcLogLikelihood function (discussed next) adds the log-likelihoods computed for each instance together to yield the overall log-likelihood.
I will describe in detail below only the unpartitioned case.
The only remaining BeagleLib function that needs to be called is beagleCalculateEdgeLogLikelihoods. We have computed partials for the tree down to the bottom-most internal node (node 7 in the examples shown in Figs. 10.1 and 10.2), which will be considered the “parent” in the beagleCalculateEdgeLogLikelihoods function call (even though it is actually the only descendant of the root). The leaf node serving as the root (node 0 in the examples shown in Figs. 10.1 and 10.2) in this unrooted tree will be considered the “child” in the beagleCalculateEdgeLogLikelihoods function call. There is thus one edge left that has not been accounted for, and that is the edge connecting the parent to the child.
The 13 arguments supplied to the beagleCalculateEdgeLogLikelihoods function are:
Instance
This must be a valid BeagleLib instance.
List of indices of parent partials buffers
In our case, the list has only one element, which is the index of the parent node (the internal node having index 7).
List of indices of child partials buffers
In our case, the list has only one element, which is the index of the child node (the leaf having index 0).
List of indices of transition probability matrices for this edge
In our case, the list has only one element, which is the index of the child node.
List of indices of first derivative matrices
We do not need to calculate first derivatives, so NULL is supplied for this.
List of indices of second derivative matrices
We do not need to calculate second derivatives, so NULL is supplied for this.
List of indices of weights to apply to each partials buffer
This list supplies the relative rates and probabilities, of which there is only one set in our case, so we supply the index 0 here.
List of indices of state frequencies for each partials buffer
This list supplies the state frequencies, of which there is only one set in our case, so we supply the index 0 here.
List of indices of scale buffers containing accumulated factors to apply to each partials buffer
Because we are not protecting site likelihoods from underflow yet, we supply BEAGLE_OP_NONE here.
Number of partials buffers
This is the number of elements in each of the lists supplied above. In our case, the number of partials buffers is just 1.
Destination for log-likelihood value
This is the address of a
doublevalue in which will be stored the final log-likelihood.
Destination for first derivative value
This is the address of a
doublevalue in which will be stored the first derivative (we supply NULL because we do not need first derivatives to be calculated).
Destination for second derivative value
This is the address of a
doublevalue in which will be stored the second derivative (we supply NULL because we do not need second derivatives to be calculated).
Here is the function body:
inline double Likelihood::calcInstanceLogLikelihood(InstanceInfo & info, Tree::SharedPtr t) {
int code = 0;
unsigned nsubsets = (unsigned)info.subsets.size();
assert(nsubsets > 0);
// Assuming there are as many transition matrices as there are edge lengths
assert(_pmatrix_index[info.handle].size() == _edge_lengths[info.handle].size());
int state_frequency_index = 0;
int category_weights_index = 0;
int cumulative_scale_index = BEAGLE_OP_NONE;
int child_partials_index = getPartialIndex(t->_root, info);
int parent_partials_index = getPartialIndex(t->_preorder[0], info);
int parent_tmatrix_index = getTMatrixIndex(t->_preorder[0], info, 0);
// storage for results of the likelihood calculation
std::vector<double> subset_log_likelihoods(nsubsets, 0.0);
double log_likelihood = 0.0;
if (nsubsets > 1) {
_parent_indices.assign(nsubsets, parent_partials_index);
_child_indices.assign(nsubsets, child_partials_index);
_weights_indices.assign(nsubsets, category_weights_index);
_scaling_indices.resize(nsubsets);
_subset_indices.resize(nsubsets);
_freqs_indices.resize(nsubsets);
_tmatrix_indices.resize(nsubsets);
for (unsigned s = 0; s < nsubsets; s++) {
_scaling_indices[s] = BEAGLE_OP_NONE;
_subset_indices[s] = s;
_freqs_indices[s] = s;
_tmatrix_indices[s] = getTMatrixIndex(t->_preorder[0], info, s); //index_focal_child + s*tmatrix_skip;
}
code = beagleCalculateEdgeLogLikelihoodsByPartition(
info.handle, // instance number
&_parent_indices[0], // indices of parent partialsBuffers
&_child_indices[0], // indices of child partialsBuffers
&_tmatrix_indices[0], // transition probability matrices for this edge
NULL, // first derivative matrices
NULL, // second derivative matrices
&_weights_indices[0], // weights to apply to each partialsBuffer
&_freqs_indices[0], // state frequencies for each partialsBuffer
&_scaling_indices[0], // scaleBuffers containing accumulated factors
&_subset_indices[0], // indices of subsets
nsubsets, // partition subset count
1, // number of distinct eigen decompositions
&subset_log_likelihoods[0], // address of vector of log likelihoods (one for each subset)
&log_likelihood, // destination for resulting log likelihood
NULL, // destination for vector of first derivatives (one for each subset)
NULL, // destination for first derivative
NULL, // destination for vector of second derivatives (one for each subset)
NULL); // destination for second derivative
}
else {
code = beagleCalculateEdgeLogLikelihoods(
info.handle, // instance number
&parent_partials_index, // indices of parent partialsBuffers
&child_partials_index, // indices of child partialsBuffers
&parent_tmatrix_index, // transition probability matrices for this edge
NULL, // first derivative matrices
NULL, // second derivative matrices
&category_weights_index, // weights to apply to each partialsBuffer
&state_frequency_index, // state frequencies for each partialsBuffer
&cumulative_scale_index, // scaleBuffers containing accumulated factors
1, // Number of partialsBuffer
&log_likelihood, // destination for log likelihood
NULL, // destination for first derivative
NULL); // destination for second derivative
}
if (code != 0)
throw XStrom(boost::str(boost::format("failed to calculate edge logLikelihoods in CalcLogLikelihood. BeagleLib error code was %d (%s)") % code % _beagle_error[code]));
return log_likelihood;
}
The calcLogLikelihood member function
The final member function we need to define is the one that returns the log-likelihood for a tree. For now, we only consider unrooted trees, so the beginning of this function is concerned with ensuring that this is true. After that, the member functions setModelRateMatrix, setAmongSiteRateHeterogenetity, defineOperations, updateTransitionMatrices and calculatePartials are called: see the description of those functions above for an explanation of what they do.
After everything is set up, all that is left to do is call the calcInstanceLogLikelihood member function, which returns the log-likelihood for just the data managed by a single BeagleLib instance. These instance-specific log-likelihoods are added together to produce the overall log-likelihood, which is then returned.
inline double Likelihood::calcLogLikelihood(Tree::SharedPtr t) {
assert(_instances.size() > 0);
if (!_using_data)
return 0.0;
// Must call setData before calcLogLikelihood
assert(_data);
if (t->_is_rooted)
throw XStrom("This version of the program can only compute likelihoods for unrooted trees");
// Assuming "root" is leaf 0
assert(t->_root->_number == 0 && t->_root->_left_child == t->_preorder[0] && !t->_preorder[0]->_right_sib);
setModelRateMatrix();
setAmongSiteRateHeterogenetity();
defineOperations(t);
updateTransitionMatrices();
calculatePartials();
double log_likelihood = 0.0;
for (auto & info : _instances) {
log_likelihood += calcInstanceLogLikelihood(info, t);
}
return log_likelihood;
}