The ASRV class handles everything associated with among-site rate heterogeneity for the Model. The Model has only to provide the variance among rates and the ASRV object recalculates the rate category boundaries and discrete gamma rate category means. Hiding the details of rate heterogeneity in this way makes it easy to later swap in a different version of ASRV that does not use the discrete gamma distribution to model among-site rate heterogeneity.
Begin by creating a new header file named asrv.hpp to contain the ASRV class declaration and member function bodies:
#pragma once
#include <vector>
#include <boost/math/distributions/gamma.hpp>
namespace strom {
class ASRV {
public:
typedef std::vector<double> rate_prob_t;
typedef std::shared_ptr<double> relrate_ptr_t;
typedef std::shared_ptr<double> ratevar_ptr_t;
typedef std::shared_ptr<double> pinvar_ptr_t;
typedef std::shared_ptr<ASRV> SharedPtr;
ASRV();
virtual ~ASRV();
void clear();
void setNumCateg(unsigned ncateg);
unsigned getNumCateg() const;
void setRateVarSharedPtr(ratevar_ptr_t ratevar);
void setRateVar(double v);
const ratevar_ptr_t getRateVarSharedPtr() const;
double getRateVar() const;
void fixRateVar(bool is_fixed);
bool isFixedRateVar() const;
void setPinvarSharedPtr(pinvar_ptr_t pinvar);
void setPinvar(double p);
const pinvar_ptr_t getPinvarSharedPtr() const;
double getPinvar() const;
void fixPinvar(bool is_fixed);
bool isFixedPinvar() const;
void setIsInvarModel(bool is_invar_model);
bool getIsInvarModel() const;
const double * getRates() const;
const double * getProbs() const;
private:
virtual void recalcASRV();
unsigned _num_categ;
bool _invar_model;
ratevar_ptr_t _ratevar;
pinvar_ptr_t _pinvar;
bool _ratevar_fixed;
bool _pinvar_fixed;
rate_prob_t _rates;
rate_prob_t _probs;
};
// Member function bodies go here
}
The constructor, destructor, and clear function
The constructor and destructor are routine, and the clear function simply sets the number of rate categories to 1 (i.e. rate homogeneity is the default).
inline ASRV::ASRV() {
//std::cout << "Constructing a ASRV" << std::endl;
clear();
}
inline ASRV::~ASRV() {
//std::cout << "Destroying a ASRV" << std::endl;
}
inline void ASRV::clear() {
// Rate homogeneity is the default
_invar_model = false;
_ratevar_fixed = false;
_pinvar_fixed = false;
_ratevar = std::make_shared<double>(1.0);
_pinvar = std::make_shared<double>(0.0);
_num_categ = 1;
recalcASRV();
}
The getRateVarSharedPtr member function
Returns the shared pointer _ratevar, which points to the double value storing the variance of rates across sites.
inline const ASRV::ratevar_ptr_t ASRV::getRateVarSharedPtr() const {
return _ratevar;
}
The getRateVar member function
Returns the double value stored at the shared pointer _ratevar, which represents the variance of rates across sites.
inline double ASRV::getRateVar() const {
assert(_ratevar);
return *_ratevar;
}
The getPinvarSharedPtr member function
Returns the shared pointer _pinvar, which points to the double value storing the proportion of invariable sites.
inline const ASRV::pinvar_ptr_t ASRV::getPinvarSharedPtr() const {
return _pinvar;
}
The getPinvar member function
Returns the double value at the shared pointer _pinvar, which represents the proportion of invariable sites.
inline double ASRV::getPinvar() const {
assert(_pinvar);
return *_pinvar;
}
The getRates member function
Returns a pointer to the array of rates stored in the vector _rates.
inline const double * ASRV::getRates() const {
return &_rates[0];
}
The getProbs member function
Returns a pointer to the array of rate probabilities stored in the vector _probs.
inline const double * ASRV::getProbs() const {
return &_probs[0];
}
The getIsInvarModel member function
Returns the value of _invar_model. which determines whether this is an invariable sites model.
inline bool ASRV::getIsInvarModel() const {
return _invar_model;
}
The getNumCateg member function
Returns the number of rate categories, _num_categ.
inline unsigned ASRV::getNumCateg() const {
return _num_categ;
}
The setNumCateg member function
This function sets the number of rate categories (_num_categ) and calls recalcASRV to recompute rate category boundaries, rate category probabilities, and category mean rates.
inline void ASRV::setNumCateg(unsigned ncateg) {
_num_categ = ncateg;
recalcASRV();
}
The setRateVarSharedPtr member function
This function assigns a shared pointer to the variance of rates across sites to the data member _ratevar.
inline void ASRV::setRateVarSharedPtr(ratevar_ptr_t ratevar) {
_ratevar = ratevar;
recalcASRV();
}
The setRateVar member function
This function sets the value of the variance of rates across sites, pointed to by the data member _ratevar.
inline void ASRV::setRateVar(double v) {
*_ratevar = v;
recalcASRV();
}
The setPinvarSharedPtr member function
This function assigns a shared pointer to the proportion of invariable sites to the data member _pinvar.
inline void ASRV::setPinvarSharedPtr(pinvar_ptr_t pinvar) {
_pinvar = pinvar;
recalcASRV();
}
The setPinvar member function
This function sets the value of the proportion of invariable sites, pointed to by the data member _pinvar.
inline void ASRV::setPinvar(double p) {
*_pinvar = p;
recalcASRV();
}
The setIsInvarModel member function
This function sets the _invar_model data member, a bool value that determines whether this ASRV object will represent the invariable sites model.
inline void ASRV::setIsInvarModel(bool is_invar_model) {
_invar_model = is_invar_model;
recalcASRV();
}
The fixRateVar, fixPinvar, isFixedRateVar, and isFixedPinvar member functions
The first 2 of these functions set the _ratevar_fixed and _pinvar_fixed data members, respectively. Each stores a bool value that determines whether their particular model parameter will be fixed or allowed to vary in, say, an MCMC analysis. The second set of 2 functions serve as accessors for these bool values.
inline void ASRV::fixRateVar(bool is_fixed) {
_ratevar_fixed = is_fixed;
}
inline void ASRV::fixPinvar(bool is_fixed) {
_pinvar_fixed = is_fixed;
}
inline bool ASRV::isFixedRateVar() const {
return _ratevar_fixed;
}
inline bool ASRV::isFixedPinvar() const {
return _pinvar_fixed;
}
The recalcASRV member function
Discrete Gamma Rate Heterogeneity (+G model)
This function recomputes several vectors related to modeling discrete-gamma among-site rate variation. The relative rate of a nucleotide site is the ratio of its rate of substitution to the average rate. A relative rate equal to 1.0 means that the site is evolving at exactly the average rate, while a relative rate of 2.0 means that site is evolving at twice the average rate. Relative rates are assumed to follow a Gamma distribution with mean 1.0 and shape 1/_ratevar.
A Gamma(α,β) distribution having shape α and scale β has mean αβ. Because the mean relative rate should be 1.0, this implies that β = 1/α, so the scale parameter α completely determines the Gamma distribution. Because the variance of a Gamma(α,β) distribution is α β2 = α(1/α)(1/α) = 1/α, it makes sense to specify the variance of rates across sites (_ratevar) and determine the shape parameter α as 1/_ratevar. Rate heterogeneity is thus proportional to _ratevar, and _ratevar equal to zero corresponds to no rate heterogeneity.
The Gamma distribution is partitioned into _num_categ subsets having equal area under the probability density curve (and thus equal probability), and the mean of each category serves as the relative rate representing that category. Rate heterogeneity is thus modeled as a discrete mixture distribution with each component of the mixture having equal probability (i.e. representing the same proportion of sites).
The mean of one category is computed as follows:
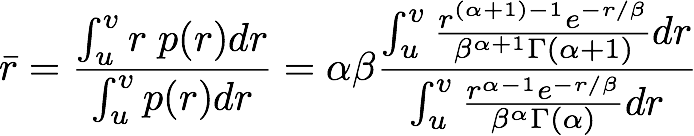
This involves a ratio of integrals of two Gamma distributions. The Gamma distribution in the numerator has shape α + 1, while the Gamma distribution in the denominator has shape α, and both have scale β = 1/α. The values u and v define the boundaries of the category for which the mean is being calculated. Calcluation of these two integrals is done using the quantile and cdf functions for the Gamma distribution provided by the Boost Math library.
Invariable Sites (+I model)
The ASRV class also allows a rate heterogeneity model to allow a fraction of sites (determined by the proportion of invariable sites _pinvar parameter) to be invariable (rate of substitution equal to zero). Adding invariable sites capability involves adding an additional rate (equal to 0.0) and and additional rate category (having probability pinvar). The remaining _ncateg categories no longer have probability equal to 1/_ncateg because their sum must now equal 1 - pinvar. Making the probability of each non-zero rate category equal to (1-pinvar)/ncateg accomplishes this.
Here is the code for handling calculation of the rates and probabilities under the +G or +I+G models:
inline void ASRV::recalcASRV() {
// This implementation assumes discrete gamma among-site rate heterogeneity
// using a _num_categ category discrete gamma distribution with equal category
// probabilities and Gamma density with mean 1.0 and variance _rate_var.
// If _invar_model is true, then rate probs will sum to 1 - _pinvar rather than 1
// and the mean rate will be 1/(1 - _pinvar) rather than 1; the rest of the invariable
// sites component of the model is handled outside the ASRV class.
// _num_categ, _rate_var, and _pinvar must all have been assigned in order to compute rates and probs
if ( (!_ratevar) || (!_num_categ) || (!_pinvar) )
return;
double pinvar = *_pinvar;
assert(pinvar >= 0.0);
assert(pinvar < 1.0);
assert(_num_categ > 0);
double equal_prob = 1.0/_num_categ;
double mean_rate_variable_sites = 1.0;
if (_invar_model)
mean_rate_variable_sites /= (1.0 - pinvar);
_rates.assign(_num_categ, mean_rate_variable_sites);
_probs.assign(_num_categ, equal_prob);
double rate_variance = *_ratevar;
assert(rate_variance >= 0.0);
if (_num_categ == 1 || rate_variance == 0.0)
return;
double alpha = 1.0/rate_variance;
double beta = rate_variance;
boost::math::gamma_distribution<> my_gamma(alpha, beta);
boost::math::gamma_distribution<> my_gamma_plus(alpha + 1.0, beta);
double cum_upper = 0.0;
double cum_upper_plus = 0.0;
double upper = 0.0;
double cum_prob = 0.0;
for (unsigned i = 1; i <= _num_categ; ++i) {
double cum_lower_plus = cum_upper_plus;
double cum_lower = cum_upper;
cum_prob += equal_prob;
if (i < _num_categ) {
upper = boost::math::quantile(my_gamma, cum_prob);
cum_upper_plus = boost::math::cdf(my_gamma_plus, upper);
cum_upper = boost::math::cdf(my_gamma, upper);
}
else {
cum_upper_plus = 1.0;
cum_upper = 1.0;
}
double numer = cum_upper_plus - cum_lower_plus;
double denom = cum_upper - cum_lower;
double r_mean = (denom > 0.0 ? (alpha*beta*numer/denom) : 0.0);
_rates[i-1] = r_mean*mean_rate_variable_sites;
}
}