Run the program using this strom.conf file.
datafile = rbcl10.nex
treefile = rbcl10.tre
subset = first:1-1314\3
subset = second:2-1314\3
subset = third:3-1314\3
statefreq = default:0.294667,0.189172,0.206055,0.310106
rmatrix = default:0.06082,0.27887,0.06461,0.06244,0.48492,0.04834
ratevar = default:1.0
ratevar = third:1.0
pinvar = default:0.1
pinvar = third:0.1
ncateg = default:4
relrate = default:1,2,3
niter = 10000
samplefreq = 10
printfreq = 100
expectedLnL = -6676.396
This time take a look at the file trees.tre and note how the tree topology and edge lengths vary during the run. You may wish to load the tree file into the program FigTree to view the trees.
Exploring the prior
A good way to test Bayesian MCMC software is to allow the program to explore the prior rather than the posterior. Because the prior is known, this provides a good sanity check of the MCMC machinery.
Modify the Strom::run function, adding just the one line highlighted in bold, blue text. The default behavior is to use data if it is available (see the Likelihood::clear function). The line we’re adding sets Likelihood::_using_data to false, which causes the Likelihood::calcLogLikelihood to always return 0.0 rather than computing the log-likelihood.
inline void Strom::run() {
std::cout << "Starting..." << std::endl;
std::cout << "Current working directory: " << boost::filesystem::current_path() << std::endl;
try {
std::cout << "\n*** Reading and storing the data in the file " << _data_file_name << std::endl;
_data = Data::SharedPtr(new Data());
_data->setPartition(_partition);
_data->getDataFromFile(_data_file_name);
_model->setSubsetNumPatterns(_data->calcNumPatternsVect());
_model->setSubsetSizes(_partition->calcSubsetSizes());
_model->activate();
// Report information about data partition subsets
unsigned nsubsets = _data->getNumSubsets();
std::cout << "\nNumber of taxa: " << _data->getNumTaxa() << std::endl;
std::cout << "Number of partition subsets: " << nsubsets << std::endl;
for (unsigned subset = 0; subset < nsubsets; subset++) {
DataType dt = _partition->getDataTypeForSubset(subset);
std::cout << " Subset " << (subset+1) << " (" << _data->getSubsetName(subset) << ")" << std::endl;
std::cout << " data type: " << dt.getDataTypeAsString() << std::endl;
std::cout << " sites: " << _data->calcSeqLenInSubset(subset) << std::endl;
std::cout << " patterns: " << _data->getNumPatternsInSubset(subset) << std::endl;
std::cout << " ambiguity: " << (_ambig_missing || dt.isCodon() ? "treated as missing data (faster)" : "handled appropriately (slower)") << std::endl;
}
std::cout << "\n*** Model description" << std::endl;
std::cout << _model->describeModel() << std::endl;
std::cout << "\n*** Creating the likelihood calculator" << std::endl;
_likelihood = Likelihood::SharedPtr(new Likelihood());
_likelihood->setPreferGPU(_use_gpu);
_likelihood->setAmbiguityEqualsMissing(_ambig_missing);
_likelihood->setData(_data);
_likelihood->useUnderflowScaling(_use_underflow_scaling);
_likelihood->setModel(_model);
_likelihood->initBeagleLib();
std::cout << "\n*** Resources available to BeagleLib " << _likelihood->beagleLibVersion() << ":\n";
std::cout << "Preferred resource: " << (_use_gpu ? "GPU" : "CPU") << std::endl;
std::cout << "Available resources:" << std::endl;
std::cout << _likelihood->availableResources() << std::endl;
std::cout << "Resources used:" << std::endl;
std::cout << _likelihood->usedResources() << std::endl;
std::cout << "\n*** Reading and storing tree number " << (_model->getTreeIndex() + 1) << " in the file " << _tree_file_name << std::endl;
_tree_summary = TreeSummary::SharedPtr(new TreeSummary());
_tree_summary->readTreefile(_tree_file_name, 0);
Tree::SharedPtr tree = _tree_summary->getTree(_model->getTreeIndex());
std::string newick = _tree_summary->getNewick(_model->getTreeIndex());
if (tree->numLeaves() != _data->getNumTaxa())
throw XStrom(boost::format("Number of taxa in tree (%d) does not equal the number of taxa in the data matrix (%d)") % tree->numLeaves() % _data->getNumTaxa());
std::cout << "\n*** Calculating the likelihood of the tree" << std::endl;
TreeManip tm(tree);
tm.selectAllPartials();
tm.selectAllTMatrices();
double lnL = _likelihood->calcLogLikelihood(tree);
tm.deselectAllPartials();
tm.deselectAllTMatrices();
std::cout << boost::str(boost::format("log likelihood = %.5f") % lnL) << std::endl;
if (_expected_log_likelihood != 0.0)
std::cout << boost::str(boost::format(" (expecting %.3f)") % _expected_log_likelihood) << std::endl;
// Create a Lot object that generates (pseudo)random numbers
_lot = Lot::SharedPtr(new Lot);
_lot->setSeed(_random_seed);
// Create an output manager and open output files
_output_manager.reset(new OutputManager);
<span style="color:#0000ff"><strong>_likelihood->useStoredData(false);</strong></span>
// Create a Chain object and take _num_iter steps
Chain chain;
unsigned num_free_parameters = chain.createUpdaters(_model, _lot, _likelihood);
if (num_free_parameters > 0) {
_output_manager->outputConsole(boost::str(boost::format("\n%12s %12s %12s %12s") % "iteration" % "logLike" % "logPrior" % "TL"));
_output_manager->openTreeFile("trees.tre", _data);
_output_manager->openParameterFile("params.txt", _model);
chain.setTreeFromNewick(newick);
chain.start();
sample(0, chain);
for (unsigned iteration = 1; iteration <= _num_iter; ++iteration) {
chain.nextStep(iteration);
sample(iteration, chain);
}
chain.stop();
// Close output files
_output_manager->closeTreeFile();
_output_manager->closeParameterFile();
// Summarize updater efficiency
_output_manager->outputConsole("\nChain summary:");
std::vector<std::string> names = chain.getUpdaterNames();
std::vector<double> lambdas = chain.getLambdas();
std::vector<double> accepts = chain.getAcceptPercentages();
std::vector<unsigned> nupdates = chain.getNumUpdates();
unsigned n = (unsigned)names.size();
_output_manager->outputConsole(boost::str(boost::format("%30s %15s %15s %15s") % "Updater" % "Tuning Param." % "Accept %" % "No. Updates"));
for (unsigned i = 0; i < n; ++i) {
_output_manager->outputConsole(boost::str(boost::format("%30s %15.3f %15.1f %15d") % names[i] % lambdas[i] % accepts[i] % nupdates[i]));
}
}
else {
_output_manager->outputConsole("MCMC skipped because there are no free parameters in the model");
}
}
catch (XStrom & x) {
std::cerr << "Strom encountered a problem:\n " << x.what() << std::endl;
}
std::cout << "\nFinished!" << std::endl;
}
Bump up the number of iterations (niter) in the strom.conf file to 100,000 in order to get an extremely good sample:
niter = 100000
Run the program again and view the results in Tracer.
Check the tree length prior
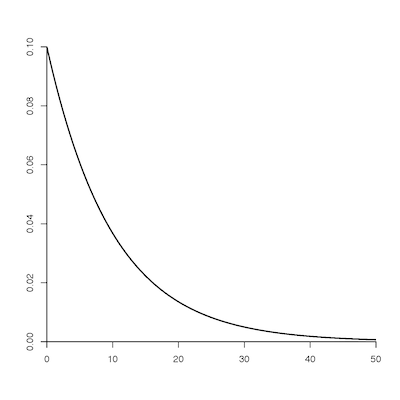 In Tracer, bring the panel labeled “Marginal Density” to the front and click on “TL” in the Traces list. We specified the tree length prior to be Exponential with mean 10. To the right is a plot of this density for comparison. Because Tracer approximates the density using a generic kernel density estimator, which does not take into account the fact that an exponential 0.1 density must have height 0.1 at 0.0, the density shown in Tracer will not exactly fit the plot, but it should be close except for the gap on the left end.
In Tracer, bring the panel labeled “Marginal Density” to the front and click on “TL” in the Traces list. We specified the tree length prior to be Exponential with mean 10. To the right is a plot of this density for comparison. Because Tracer approximates the density using a generic kernel density estimator, which does not take into account the fact that an exponential 0.1 density must have height 0.1 at 0.0, the density shown in Tracer will not exactly fit the plot, but it should be close except for the gap on the left end.
Switch to the “Estimates” panel while still selecting TL in Traces: the mean of the distribution should be close to 10 and the variance close to 100.
Check the subset relative rates
The subset relative rates have a prior distribution related to Dirichlet(1,1,1). The difference lies in the fact that it is the product of subset rates and subset proportions that is distributed as Dirichlet(1,1,1), not the rates themselves. Select all three subset relative rates (m-0, m-1, and m-2) under Traces on the left. These three densities should be nearly identical (“Marginal Density” panel), and they should all have means close to 1.0 and variances close to 0.5.
Check the state frequencies
The state frequencies have prior Dirichlet(1,1,1,1). This is a flat Dirichlet distribution. Each component of a flat Dirichlet has variance equal to
variance of one component = (1/n)*(1 - 1/n)/(n + 1)
where n is the number of dimensions (i.e. the number of Dirichlet parameters). For nucleotide state frequencies, n = 4 so the variance of one component should equal (1/4)(3/4)/5 = 3/80 = 0.0375. Being flat, each state frequency has the same probability as any other state frequency, so the mean for each should be 1/4 = 0.25.
Select all 4 state frequencies for any subset (e.g. piA-0, piC-0, piG-0, and piT-0) under Traces on the left. These 4 densities should be nearly identical (“Marginal Density” panel), and they should all have means close to 1/4 and variances close to 0.0375.
Check the exchangeabilities
The exchangeabilities have prior Dirichlet(1,1,1,1,1,1). Select all 6 exchangeabilities for any subset (e.g. rAC-0, rAG-0, rAT-0, rCG-0, rCT-0, and rGT-0) under Traces on the left. These 6 densities should be nearly identical (“Marginal Density” panel), and they should all have means close to 0.167 and variances close to 0.0198. These values can be obtained using the formula given above with n = 6 rather than n = 4.
Check pinvar
The pinvar parameter has prior Beta(1,1), which is just a special case of a flat Dirichlet distribution. Hence, using n = 2, we find that pinvar should have mean 0.5 and variance (1/2)(1/2)/3 = 1/12 = 0.0833. Again, Tracer may not do well near 0 and 1 with this density due to the fact that it is using a “black-box” density estimator that doesn’t know that the density should drop to exactly 0.0 at pinvar values of 0.0 and 1.0.
Check the rate variance
Finally, the rate variance parameter has prior Exponential(1), which has mean 1 and variance 1.
On to heated chains
The next step of the tutorial will introduce multiple chains (Metropolis coupling) to the MCMC analysis to improve mixing. We will also add a program option (usedata) to make ignoring data (exploring the prior) easy.