We need a new updater that either adds an edge to an existing polytomy or deletes an edge to create a new polytomy (or expand an existing one). Create the PolytomyUpdater class declaration below in the file polytomy_updater.hpp.
#pragma once
#include "updater.hpp"
namespace strom {
class Chain;
class PolytomyUpdater : public Updater {
friend class Chain;
public:
typedef std::vector<double> _partition_vect_t;
typedef std::map<unsigned, _partition_vect_t > _partition_map_t;
typedef std::vector<Node *> _polytomy_vect_t;
typedef std::shared_ptr< PolytomyUpdater > SharedPtr;
PolytomyUpdater();
~PolytomyUpdater();
virtual double calcLogPrior();
private:
virtual void revert();
virtual void proposeNewState();
virtual void reset();
void proposeAddEdgeMove(Node * nd);
void proposeDeleteEdgeMove(Node * nd);
_partition_vect_t & computePolytomyDistribution(unsigned nspokes);
void refreshPolytomies();
_partition_map_t _poly_prob;
_polytomy_vect_t _polytomies;
Node * _orig_par;
Node * _orig_lchild;
Node * _first_child;
Node * _chosen_node;
double _chosen_edgelen;
double _chosen_proportion;
double _remainder_proportion;
double _fraction;
bool _add_edge_proposed;
double _new_edge_proportion;
double _orig_edge_proportion;
double _tree_length;
double _phi;
unsigned _polytomy_size;
unsigned _num_polytomies;
};
// Member function bodies go here
}
The constructor and destructor
This class uses the base class (Updater) version of the clear function in the constructor and, as usual, the destructor has no work to do.
inline PolytomyUpdater::PolytomyUpdater() {
// std::cout << "Creating a PolytomyUpdater" << std::endl;
Updater::clear();
_name = "Polytomies";
reset();
}
inline PolytomyUpdater::~PolytomyUpdater() {
// std::cout << "Destroying a PolytomyUpdater" << std::endl;
}
The reset member function
The reset function is called at the end of the Updater::update function to prepare the updater for the next update. Any temporary variables needed by an updater during the update process need to be re-initialized in this function, and this PolytomyUpdater has several of these temporary variables, most of which are needed to keep track of how to revert if the proposed tree is rejected.
inline void PolytomyUpdater::reset() {
_tree_length = 0.0;
_new_edge_proportion = 0.0;
_orig_edge_proportion = 0.0;
_orig_par = 0;
_orig_lchild = 0;
_chosen_node = 0;
_first_child = 0;
_polytomy_size = 0;
_num_polytomies = 0;
_add_edge_proposed = false;
_polytomies.clear();
}
The calcLogPrior member function
The calcLogPrior function calls two functions in the base class (Updater) and returns the sum of the values they calculate. This function is an abstract function in the base class (along with proposeNewState and revert) and so must be defined in this derived class.
inline double PolytomyUpdater::calcLogPrior() {
double log_prior = 0.0;
log_prior += Updater::calcLogTopologyPrior();
log_prior += Updater::calcLogEdgeLengthPrior();
return log_prior;
}
The proposeNewState member function
The proposeNewState function, which is an abstract base class member function that must be defined in any derived class, proposes either an add-edge or a delete-edge move.
The first part of this function is involved in determining whether the current tree is the star tree (in which case add-edge is the only move possible) or a fully-resolved, binary tree (in which case delete-edge is the only option). If both add-edge and delete-edge are possible, then a coin flip is used to decide which of the two will be attempted.
The member functions proposeAddEdgeMove and proposeDeleteEdgeMove handle most of the work, once the decision is made which move to attempt. The calculation of the Hastings ratio and Jacobian determinant will be discussed when these functions are introduced.
inline void PolytomyUpdater::proposeNewState() {
Tree::SharedPtr tree = _tree_manipulator->getTree();
// probability of choosing and add-edge move if both add-edge and delete-edge are possible
const double _prob_add_edge = 0.5;
// Compute number of internal nodes in a fully resolved tree
unsigned num_internals_in_fully_resolved_tree = 0;
if (tree->isRooted()) {
// remember: root node is internal because it has a left child
num_internals_in_fully_resolved_tree = tree->numLeaves();
}
else
num_internals_in_fully_resolved_tree = tree->numLeaves() - 2;
// Compute tree length before proposed move
_tree_length = _tree_manipulator->calcTreeLength();
// Determine whether starting tree is fully resolved or the star tree
unsigned num_internals_before = tree->numInternals();
//unsigned num_leaves_before = tree->numLeaves();
unsigned num_internal_edges_before = num_internals_before - (tree->isRooted() ? 2 : 1);
bool fully_resolved_before = (num_internals_in_fully_resolved_tree == num_internals_before);
bool star_tree_before = (tree->numInternals() == 1);
// Rebuild _polytomies vector, which is a vector of pointers to Node objects having more than 2 children
refreshPolytomies();
_num_polytomies = (unsigned)_polytomies.size();
// Determine whether an add edge move is proposed (alternative is a delete edge move)
if (star_tree_before)
_add_edge_proposed = true;
else if (fully_resolved_before)
_add_edge_proposed = false;
else
_add_edge_proposed = (_lot->uniform() < _prob_add_edge);
Node * nd = 0;
if (_add_edge_proposed) {
// Choose a polytomy at random to split
unsigned i = (unsigned)_lot->randint(0, _num_polytomies-1);
nd = _polytomies[i];
_polytomy_size = 1 + _tree_manipulator->countChildren(nd);
// Add an edge to split up polytomy at nd, moving a random subset
// of the spokes to the (new) left child of nd
proposeAddEdgeMove(nd);
double TL_after_add_edge = _tree_manipulator->calcTreeLength();
assert(std::fabs(_tree_length - TL_after_add_edge) < 1.e-8);
// Compute the log of the Hastings ratio
_log_hastings_ratio = 0.0;
_log_hastings_ratio += std::log(_num_polytomies);
_log_hastings_ratio += std::log(pow(2.0, _polytomy_size - 1) - _polytomy_size - 1);
_log_hastings_ratio -= std::log(num_internal_edges_before + 1);
// Now multiply by the value of the quantity labeled gamma_b in the Lewis-Holder-Holsinger (2005) paper
unsigned num_internals_after = tree->numInternals();
assert(num_internals_after == num_internals_before + 1);
const bool fully_resolved_after = (num_internals_after == num_internals_in_fully_resolved_tree);
double tmp = 0.0;
if (star_tree_before && !fully_resolved_after)
tmp += log(1.0 - _prob_add_edge);
else if (fully_resolved_after && !star_tree_before)
tmp -= log(_prob_add_edge);
else if (!star_tree_before && !fully_resolved_after) {
tmp += log(1.0 - _prob_add_edge);
tmp -= log(_prob_add_edge);
}
_log_hastings_ratio += tmp;
// Compute the log of the Jacobian
//_log_jacobian = std::log(_orig_edge_proportion) - std::log(1.-_fraction);
_log_jacobian = std::log(_orig_edge_proportion); //POLTMP temporary!
// flag partials for recalculation
_tree_manipulator->selectPartialsHereToRoot(_orig_lchild);
// These two nodes have had their edge lengths modified, so their transition matrices need recalculating
_orig_lchild->selectTMatrix();
_chosen_node->selectTMatrix();
}
else {
// Choose an internal edge at random and delete it to create a polytomy
// (or a bigger polytomy if there is already a polytomy)
nd = _tree_manipulator->randomInternalEdge(_lot);
assert(nd->getParent() && nd->getParent()->getParent());
proposeDeleteEdgeMove(nd);
double TL_after_del_edge = _tree_manipulator->calcTreeLength();
assert(std::fabs(_tree_length - TL_after_del_edge) < 1.e-8);
// Compute the log of the Hastings ratio
_log_hastings_ratio = 0.0;
_log_hastings_ratio += std::log(num_internal_edges_before);
_log_hastings_ratio -= std::log(_num_polytomies);
_log_hastings_ratio -= std::log(pow(2.0, _polytomy_size - 1) - _polytomy_size - 1);
// Now multiply by the value of the quantity labeled gamma_b in the Lewis-Holder-Holsinger (2005) paper
// Now multiply by the value of the quantity labeled gamma_d in the paper
unsigned num_internals_after = tree->numInternals();
assert(num_internals_after == num_internals_before - 1);
const bool star_tree_after = (num_internals_after == (tree->isRooted() ? 2 : 1));
double tmp = 0.0;
if (fully_resolved_before && !star_tree_after)
tmp += log(_prob_add_edge);
else if (star_tree_after && !fully_resolved_before)
tmp -= log(1.0 - _prob_add_edge);
else if (!fully_resolved_before && !star_tree_after) {
tmp += log(_prob_add_edge);
tmp -= log(1.0 - _prob_add_edge);
}
_log_hastings_ratio += tmp;
// Compute the log Jacobian
_log_jacobian = -std::log(_new_edge_proportion);
// flag partials and transition matrices for recalculation
_tree_manipulator->selectPartialsHereToRoot(_orig_par);
_chosen_node->selectTMatrix();
// This node is no longer in the tree, so we can't include it in selectPartialsHereToRoot;
// however, this node's tmatrix and partials will be trashed because it will be employed
// as a polytomy helper in the next likelihood calculation, so it needs to be flipped
// so that a revert will retain the original tmatrix and partial
_orig_lchild->selectTMatrix();
_orig_lchild->selectPartial();
}
}
The proposeAddEdgeMove member function
The add-edge move is illustrated below. This move involves choosing a polytomy uniformly at random (1/2 in the example because there are 2 polytomies to choose from), drawing a new edge proportion by multiplying the tuning parameter (_phi) by a uniform(0,1) random deviate, squeezing the previous edge proportions down to make room for the new edge, and, finally, deciding how to partition the spokes of the original polytomy between the two nodes at the ends of the newly created edge (there are 3 possible choices for a polytomy with 4 spokes: 9,10 was chosen in the example, but 8,10 and 7,10 were also possibilities).
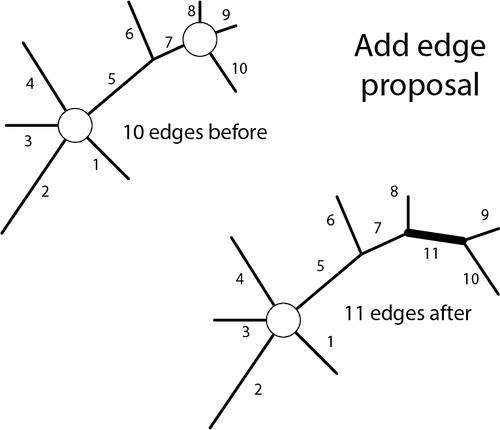
The full acceptance ratio comprises 5 terms:
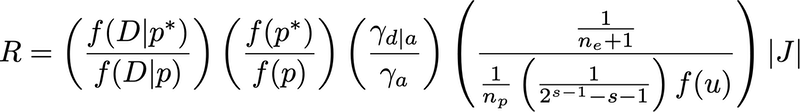
The probability of accepting the proposed add-edge move is either 1.0 or R, whichever is smaller.
The first term (left-to-right) is the likelihood ratio, which is the likelihood of the tree after the add-edge move divided by the likelihood of the tree before the move. This term is straightforward (although, as you will see shortly, we will have to modify our Likelihood class to handle computing likelihoods for polytomous trees).
The second term is the ratio of the prior density after the move divided by the prior density before the move. The prior in both cases is a product of the (discrete) topology prior probability and the edge proportions prior density. The topology prior is new, but will be discussed when we modify the Updater base class to add the member function calcLogTopologyPrior. The PolytomyUpdater::calcLogPrior function (see above) computes the joint prior, and the Updater::update function is where this function is called (before and after the proposed move).
The third term from the left is the ratio of the probability of proposing the reverse move (a delete-edge move that exactly reverses the proposed add-edge move) divided by the probability of proposing the add-edge move itself. If the current tree (before the add-edge move) is the star tree, then this ratio equals 0.5/1 = 0.5. If the current tree is a fully-resolved tree, this ratio equals 1/0.5 = 2. Otherwise, it equals 1.0.
The fourth term is the probability of the reverse move divided by the probability of the forward (add-edge) move. The reverse move involves only a choice of which edge to delete, the probability of which is just 1 divided by the number of edges in the tree (one more than the number of edges n_e in the starting tree for the add-edge move).
The forward move is more complex. First, we must choose one of n_p polytomies to break up (probability 1/n_p). Next, we must decide which of the s spokes (edges radiating from this polytomous node) to move to the newly created node. This probability is 1 divided by the number of ways of partitioning s spokes into 2 groups, ensuring that each group contains at least 2 spokes. This number of possible partitionings is quantity 2^(s-1)-s-1. Finally, we must draw a Uniform(0,1) random deviate, u, to help us choose an edge proportion to go along with the newly created node. The probability density of this is the f(u) term, which equals 1.
The final term is the absolute value of the determinant of the Jacobian matrix for the transformation of u and the n_e edge proportions before the add-edge move into the n_e+1 edge proportions in the tree after the new edge has been inserted. The calculation of the Jacobian determinant for the simplest case (4-taxon star tree) is illustrated below:
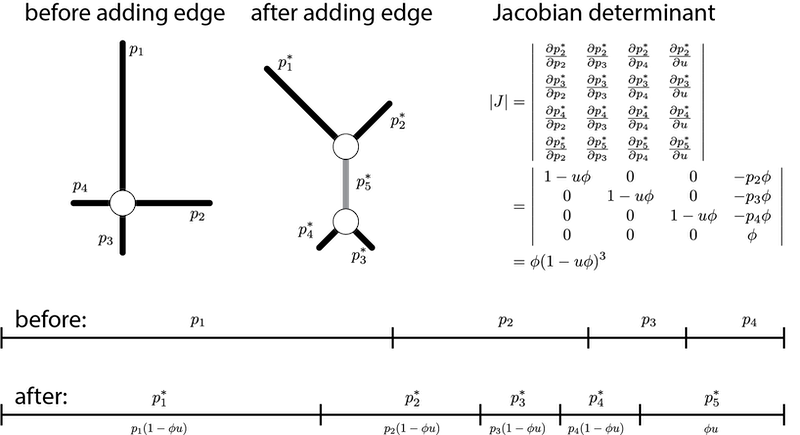
Note that the Jacobian matrix is 4x4, not 5x5, as one edge proportion can be determined from the others. I’ve arbitrarily chosen edge proportion 1 as the one that is determined by the others.
Hopefully, I’ve provided enough background for you to now understand the proposeAddEdgeMove function (and the section of proposeNewState in which it appears).
inline void PolytomyUpdater::proposeAddEdgeMove(Node * u) {
Tree::SharedPtr tree = _tree_manipulator->getTree();
// Split up the polytomy at `u' by creating a new internal node v and a new edge
// connecting u with v. Node u is saved as _orig_par and node v is saved
// as _orig_lchild in case we need to revert the proposed move.
assert(u);
// Create the new node that will receive the k randomly-chosen spokes
Node * v = _tree_manipulator->getUnusedNode();
_tree_manipulator->insertSubtreeOnLeft(v, u);
assert(u->getLeftChild() == v);
_tree_manipulator->rectifyNumInternals(+1);
// Save u and v. If revert is necessary, all of orig_lchild's nodes will be returned
// to orig_par, and orig_lchild will be deleted.
_orig_par = u;
_orig_lchild = v;
// Calculate (if necessary) the probability of each possible partitioning of the chosen polytomy
// Select number of spokes to move over to new node
// Note that 0 and 1 are not allowed because they
// would leave the tree in an invalid state
const _partition_vect_t & prob_n = computePolytomyDistribution(_polytomy_size);
double p = _lot->uniform();
double cum = 0.0;
unsigned k = 0;
bool found = false;
for (; k < prob_n.size(); ++k) {
double prob_k_given_n = prob_n[k];
cum += prob_k_given_n;
if (p < cum) {
found = true;
break;
}
}
assert(found);
k += 2;
// After the move, either _orig_par or _orig_lchild should have k spokes
// with the other node having _polytomy_size - k spokes
// (_orig_par and _orig_lchild will each have 1 additional connector spoke).
//
// Choose k spokes randomly out of the _polytomy_size available.
// If _orig_par->par is included, let _orig_par retain the k spokes and move
// _polytomy_size - k spokes to _orig_lchild.
// Otherwise, move the k spokes to _orig_lchild leaving _polytomy_size - k spokes behind.
// Create vector of valid spokes (parent and all children of _orig_par except _orig_lchild)
std::vector<Node *> uspokes;
uspokes.push_back(_orig_par->getParent());
for (Node * child = _orig_par->getLeftChild(); child; child = child->getRightSib()) {
if (child != _orig_lchild)
uspokes.push_back(child);
}
assert (uspokes.size() == _polytomy_size);
// Choose one of the candidates as the edge to break
unsigned i = (unsigned)_lot->randint(0, (int)uspokes.size()-1);
_chosen_node = uspokes[i];
if (_chosen_node == _orig_par->getParent())
_chosen_node = _orig_par;
// Break _chosen_node's edge in a random place
_orig_edge_proportion = _chosen_node->getEdgeLength()/_tree_length;
_fraction = _lot->uniform();
_new_edge_proportion = _fraction*_orig_edge_proportion;
_remainder_proportion = _orig_edge_proportion - _new_edge_proportion;
_chosen_node->setEdgeLength(_new_edge_proportion*_tree_length);
_orig_lchild->setEdgeLength(_remainder_proportion*_tree_length);
bool reverse_polarity = false;
std::vector<Node *> vspokes;
typedef std::vector<Node *>::iterator::difference_type vec_it_diff;
for (unsigned i = 0; i < k; ++i) {
unsigned num_u_spokes = (unsigned)uspokes.size();
assert(num_u_spokes > 0);
unsigned j = (unsigned)_lot->randint(0, num_u_spokes-1);
Node * s = uspokes[j];
if (s == _orig_par->getParent())
reverse_polarity = true;
vspokes.push_back(s);
uspokes.erase(uspokes.begin() + (vec_it_diff)j);
}
assert(uspokes.size() + vspokes.size() == _polytomy_size);
if (reverse_polarity) {
// transfer nodes in uspokes to _orig_lchild
for (auto s = uspokes.begin(); s != uspokes.end(); ++s) {
_tree_manipulator->detachSubtree(*s);
_tree_manipulator->insertSubtreeOnRight(*s, _orig_lchild);
}
}
else {
// transfer nodes in vspokes to _orig_lchild
for (auto s = vspokes.begin(); s != vspokes.end(); ++s) {
_tree_manipulator->detachSubtree(*s);
_tree_manipulator->insertSubtreeOnRight(*s, _orig_lchild);
}
}
_tree_manipulator->refreshNavigationPointers();
}
The proposeDeleteEdgeMove member function
The delete-edge move is illustrated below.
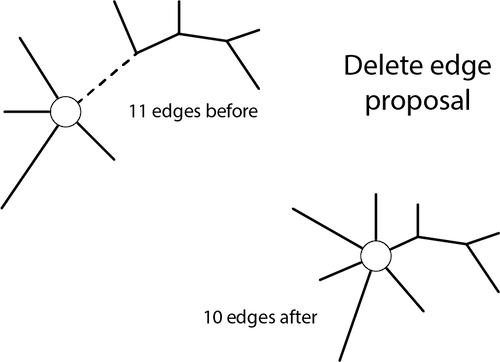
The acceptance ratio for the delete-edge move is:
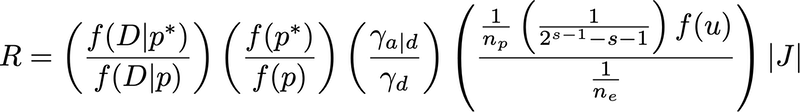
The explanation of terms is largely the same as above for the add-edge move except:
*p* now refers to the parameters after the delete-edge move and p to the parameters before the delete-edge move
- the third term equals 2 if the tree resulting from the delete-edge move is the star tree, 0.5 if the tree before the delete-edge move is fully resolved, and 1 otherwise. (Note that in the 4-taxon case the third term is always 1).
- n_p is the number of polytomies in the tree _resulting) from the delete-edge move
- s is the number of spokes in the polytomy created (or expanded) by deleting an edge
- n_e is the number of edges in the tree before the delete-edge move
- the Jacobian determinant equals 1 divided by
phi (1 - v)^(n_e-2), wherevis the proportion of the tree length corresponding to the edge that was deleted
inline void PolytomyUpdater::proposeDeleteEdgeMove(Node * v) {
// Delete the edge associated with `v' to create a polytomy (or a bigger polytomy if `v->par' was already a polytomy).
// The supplied node v should not be the only child of the root node.
//
// b c
// \ /
// \ /
// \ /
// a v a b c
// \ / \ | /
// \ / \ | /
// \ / \|/
// u u
// / /
//
// Before After
//
// Returns the number of polytomies in the tree after the proposed delete-edge move.
// The return value will be incorrect if the polytomies vector is not up-to-date.
// This operation should not leave the root node (which is a tip) with more than one
// child, so check to make sure that the supplied node is not the root nor a child of root
_orig_lchild = v;
_orig_par = _orig_lchild->getParent();
assert(_orig_par);
assert(_orig_par->getParent());
// Save _orig_lchild's edge length in case we need to revert
_orig_edge_proportion = _orig_lchild->getEdgeLength()/_tree_length;
// Compute size of polytomy after the delete-edge move, a quantity needed
// for computing the Hastings ratio. Note that one of u's children
// (i.e. _orig_lchild) is deleted but this is made up for by considering u->par,
// which is also a spoke that counts.
unsigned v_children = _tree_manipulator->countChildren(_orig_lchild);
unsigned u_children = _tree_manipulator->countChildren(_orig_par);
_polytomy_size = v_children + u_children;
bool u_polytomy_before = (u_children > 2);
bool v_polytomy_before = (v_children > 2);
if (u_polytomy_before && v_polytomy_before) {
// No. polytomies will decrease by one as a result of this delete-edge move
--_num_polytomies;
}
else if (!u_polytomy_before && !v_polytomy_before) {
// No. polytomies will increase by one as a result of this delete-edge move
++_num_polytomies;
}
// Make all of _orig_lchild's children children of _orig_par
_first_child = _orig_lchild->getLeftChild();
while (_orig_lchild->getLeftChild() != NULL) {
Node * tmp = _orig_lchild->getLeftChild();
_tree_manipulator->detachSubtree(tmp);
_tree_manipulator->insertSubtreeOnRight(tmp, _orig_par);
}
_tree_manipulator->detachSubtree(_orig_lchild);
_tree_manipulator->putUnusedNode(_orig_lchild);
_tree_manipulator->rectifyNumInternals(-1);
_tree_manipulator->refreshNavigationPointers();
// Create vector of valid spokes
std::vector<Node *> spokes;
spokes.push_back(_orig_par->getParent());
for (Node * child = _orig_par->getLeftChild(); child; child = child->getRightSib()) {
if (child != _orig_par)
spokes.push_back(child);
}
assert (spokes.size() == _polytomy_size);
// Choose one of the candidates as the edge to absorb the deleted edge
unsigned i = (unsigned)_lot->randint(0, (int)spokes.size()-1);
_chosen_node = spokes[i];
if (_chosen_node == _orig_par->getParent())
_chosen_node = _orig_par;
_chosen_edgelen = _chosen_node->getEdgeLength();
_chosen_proportion = _chosen_edgelen/_tree_length;
_chosen_node->setEdgeLength(_chosen_edgelen + _orig_edge_proportion*_tree_length);
_new_edge_proportion = _chosen_node->getEdgeLength()/_tree_length;
_fraction = _chosen_proportion/_new_edge_proportion;
}
The computePolytomyDistribution member function
The add-edge move splits the edges of a polytomy across a new edge. This function computes the probability distribution of possible partitionings and stores it in the map member variable _poly_prob under a key equal to the number of “spokes” in the polytomy where a spoke is an edge radiating from the polytomous node. The value of _poly_prob[6], as an example, is the following vector of length 2:
6!
_poly_prob[6][0] = ----- C = 3/5
2! 4!
6!
_poly_prob[6][1] = ------- C = 2/5
3! 3! 2
where C is the normalizing constant, which equals 1/(2^5 - 6 - 1) = 1/25. Note that the final probability must be divided by 2 in the case of an even number of spokes. This means that 2 of 6 spokes will be moved to the new node with probability 0.6 and 3 spokes will be moved with probability 0.4.
inline PolytomyUpdater::_partition_vect_t & PolytomyUpdater::computePolytomyDistribution(unsigned nspokes) {
assert(nspokes > 2);
// Only compute it if it isn't already stored in the _poly_prob map
auto iter = _poly_prob.find(nspokes);
if (iter == _poly_prob.end()) {
// There is no existing probability distribution vector corresponding to nspokes
double ln_denom = std::log(pow(2.0,nspokes-1) - nspokes - 1.0);
_partition_vect_t v(nspokes - 3);
unsigned first = 2;
unsigned last = nspokes/2;
bool nspokes_even = nspokes % 2 == 0;
double total_prob = 0.0;
for (unsigned x = first; x <= last; ++x) {
double ln_numer = std::lgamma(nspokes + 1) - std::lgamma(x + 1) - std::lgamma(nspokes - x + 1);
if (nspokes_even && x == last)
ln_numer -= std::log(2);
double prob_x = exp(ln_numer - ln_denom);
if (prob_x > 1.0)
prob_x = 1.0;
total_prob += prob_x;
v[x-first] = prob_x;
}
assert(std::fabs(total_prob - 1.0) < 1.e-8);
_poly_prob[nspokes] = v;
}
return _poly_prob[nspokes];
}
The revert member function
This function simply reverses the add-edge or delete-edge move performed. It is called by Updater::update if the proposed move is not accepted.
inline void PolytomyUpdater::revert() {
if (_add_edge_proposed) {
// Return all of _orig_lchild's child nodes to _orig_par, then return orig_lchild to storage
Node * child = _orig_lchild->getLeftChild();
while (child) {
Node * rsib = child->getRightSib();
_tree_manipulator->detachSubtree(child);
_tree_manipulator->insertSubtreeOnRight(child, _orig_par);
child = rsib;
}
_tree_manipulator->detachSubtree(_orig_lchild);
_tree_manipulator->putUnusedNode(_orig_lchild);
_tree_manipulator->rectifyNumInternals(-1);
_tree_manipulator->refreshNavigationPointers();
_chosen_node->setEdgeLength(_orig_edge_proportion*_tree_length);
double TL_after_revert_add_edge = _tree_manipulator->calcTreeLength();
assert(std::fabs(_tree_length -TL_after_revert_add_edge) < 1.e-8);
}
else {
Node * v = _tree_manipulator->getUnusedNode(_orig_lchild);
_tree_manipulator->rectifyNumInternals(+1);
_chosen_node->setEdgeLength(_chosen_edgelen);
v->setEdgeLength(_orig_edge_proportion*_tree_length);
for (Node * child = _first_child; child;) {
Node * child_rsib = child->getRightSib();
_tree_manipulator->detachSubtree(child);
_tree_manipulator->insertSubtreeOnRight(child, v);
child = child_rsib;
}
_tree_manipulator->insertSubtreeOnRight(v, _orig_par);
_tree_manipulator->refreshNavigationPointers();
double TL_after_revert_del_edge = _tree_manipulator->calcTreeLength();
assert(std::fabs(_tree_length - TL_after_revert_del_edge) < 1.e-8);
}
}
The refreshPolytomies member function
This function creates a vector (stored in _polytomies) of nodes that are polytomous. This is used by the add-edge move to choose a focal polytomy to split up.
inline void PolytomyUpdater::refreshPolytomies() {
Tree::SharedPtr tree = _tree_manipulator->getTree();
_polytomies.clear();
for (auto nd : tree->_preorder) {
unsigned s = _tree_manipulator->countChildren(nd);
if (s > 2)
_polytomies.push_back(nd);
}
}